Lecture 4. 역전파(Backpropagation)와 신경망(Neural Network)

해인 · November 3, 2020

CS231n

해당 포스트는 송교석 님의 유튜브 강의를 정리한 내용입니다. 강의 영상은 여기에서 보실 수 있습니다.

0. Recap

손실 함수(Loss function)

Score function $s = f(x; W) = Wx$

SVM loss $L_i = \sum_{j \ne y_i} max(0, s_j - s_{y_i} + 1)$

data loss + regularization $L = \frac{1}{N}\sum_{i=1}^{N} L_i + \sum_k W_k^2$

want $\nabla wL$

최적화(Optimization)

optimization은 loss 를 최소화 하는 값을 찾아가는 과정으로, Parameter update 라고도 한다. 이때 loss 를 최소화 하는 값을 얻어야지만 비로소 좋은 prediction이 가능합니다.

경사하강법(Gradient Decent)

gradient descent를 구하는 방법으로는 numerical gredient와 analytic gradient가 있으며 이에 대한 특징은 다음과 같습니다.

Numerical gradient: 느리고, 근삿값이지만 구현이 쉽다.
Analytic gradient: 빠르고 정확하지만 구현이 어렵다.

실제로는 analytic gradient를 구하여 사용을 하고, numerical gradient도 함께 구현하여 시작시에 값이 잘 나오는지 확인하는 gradient check를 진행합니다.

1. 계산 그래프(Computaiotnal Graph)

위의 그림은 Loss 를 구하는 과정을 간단하게 표현한 것인데, 실제로는 다음과 같이 복잡한 방식으로 Loss를 구하게 됩니다.

Convolutional Network(Alex Net)

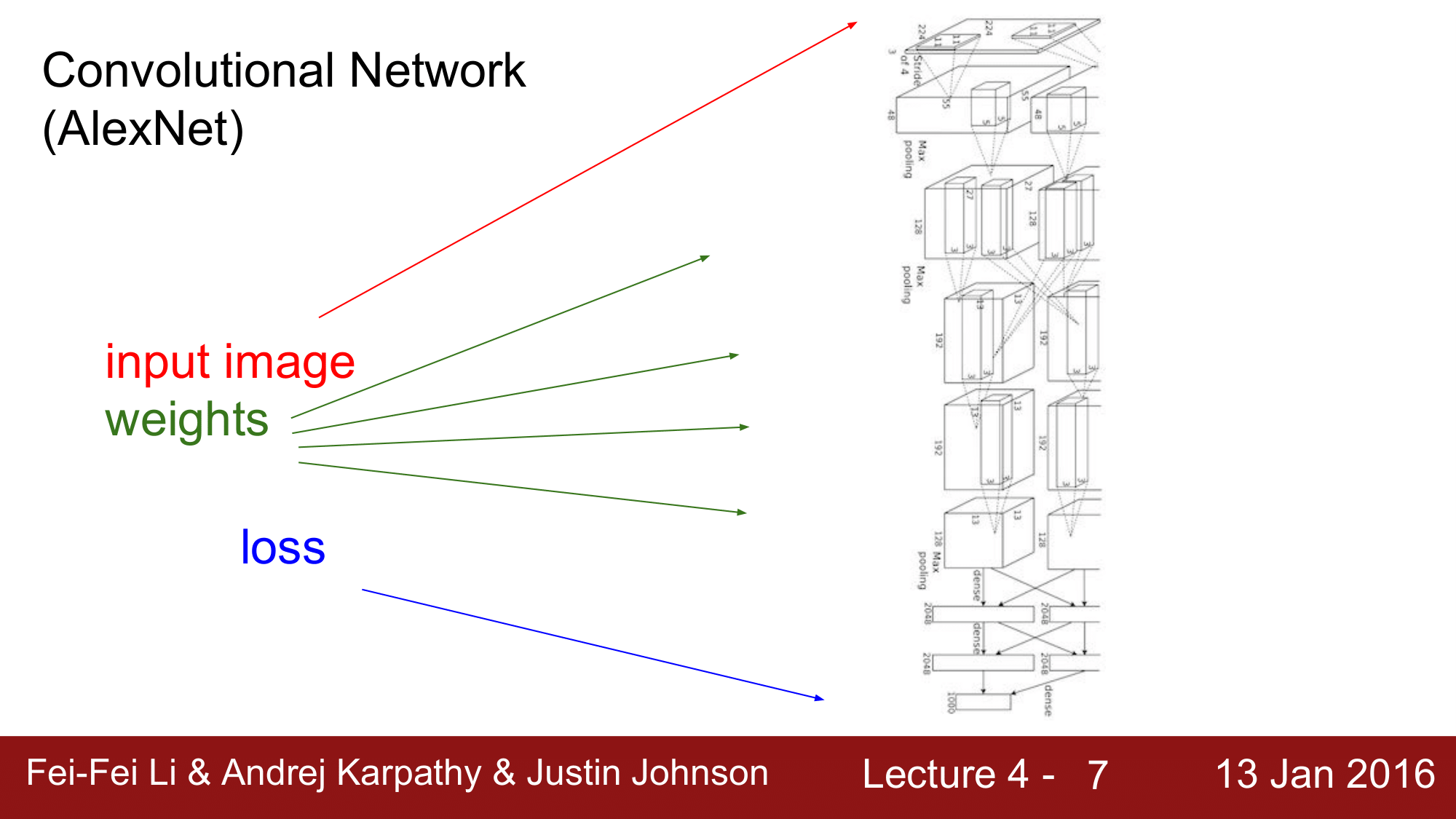
이것은 Alex Net의 모형으로, 위에서 input을 받아 복잡한 과정을 거쳐 Weight를 계산하게 되고, 결과적으로 loss를 구하게 됩니다. 보시면 아시다 싶이 이것만 해도 규모가 어느정도 되기 때문에 계산그래프로 늘어놓고 한꺼번에 계산한다는 것은 사실상 매우 힘듭니다.

Neural Turing Machine

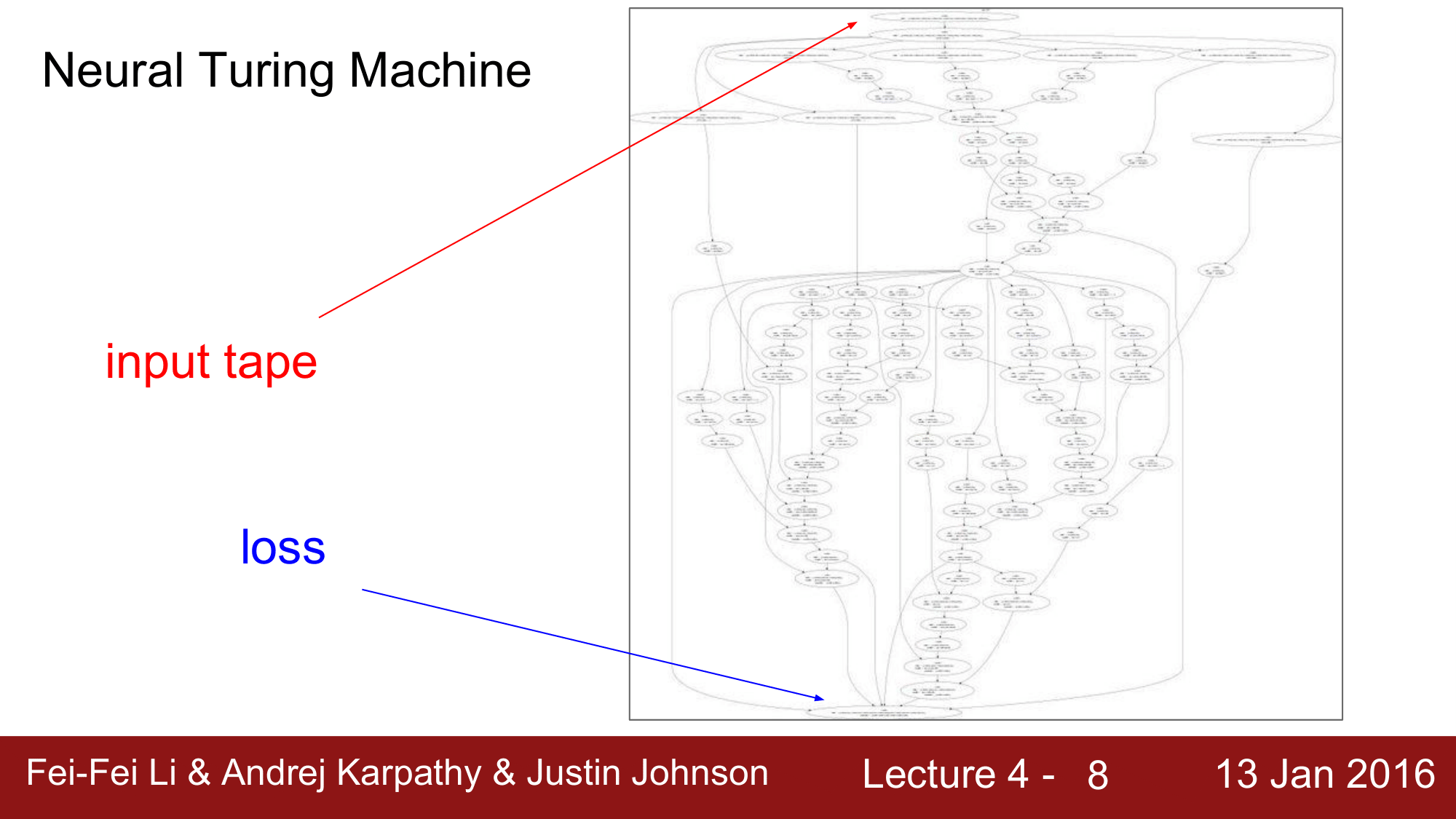
다른 모형으로 Deep Mind 에서 발표한 Neural Turing Machine을 보시게 되면, 이 또한 input를 받아 loss를 계산하는 과정이 어마어마하게 복잡한 것을 확인하실 수 있습니다.

나중에 설명하게 될 RNN(Recurrent Neural Network)의 경우 이러한 모델을 사용하게 계산을 하게 되면, 순환적으로 여러번 반복하여 계산을 하게 되기 때문에 한꺼번에 모두를 계산하는 것은 말이 안되는 일이 됩니다.

이처럼 실제로 계산그래프를 통해 한꺼번에 값을 구하는 것은 매우 어렵습니다. 따라서 계산그래프를 한꺼번에 계산하는 것이 아니라, 간단한 예를 보면서 하나씩 모듈들 별로 계산을 하는 방식으로 접근해 보겠습니다.

순방향 전파(Forward Pass; FP)

간단한 모델을 보면서 설명하기 위해 다음 수식을 가지고 하나씩 알아보겠습니다.

\[f(x, y, z) = (x + y)z \\ \\ \text{e.g.} \quad x = -2, y = 5, z = -4 \\\]

이 수식을 그림으로 표현하게 되면 다음과 같습니다.

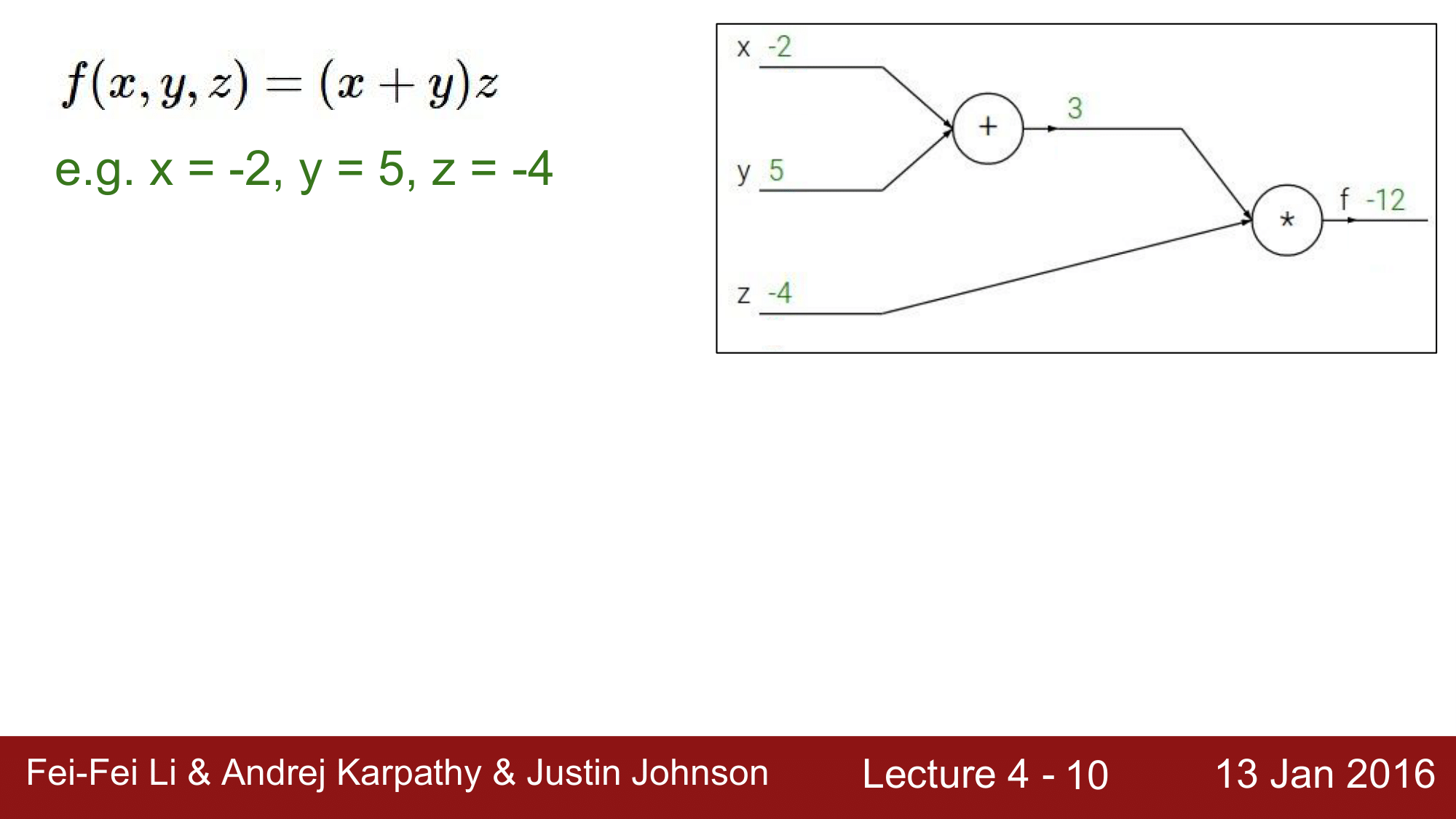
위 그림을 보통 Graph 혹은 Circuit이라고 부르는데, 그래프의 왼쪽에서 오른쪽으로 진행하는 것을 순방향 전파(Forward Pass)한다라고 합니다.

역방향 전파(Backward Pass, Backpropagation; BP)

여기서 우리가 해야하는 것은 input에 대한 gradient를 구하는 것입니다. 즉 input의 값이 마지막 단에 어느정도 영향을 미치는 것인지를 구하고 싶은 것 입니다. 이를 위해 $x + y = q$를 도입하여 각각에 대한 미분을 살펴보겠습니다.

각각을 미분하게 되면 다음과 같습니다.

\[\begin{aligned} & q = x + y \quad \frac{\partial q}{\partial x} = 1,\frac{\partial q}{\partial y} = 1 \\ & f = qz \qquad \frac{\partial f}{\partial q} = z,\frac{\partial f}{\partial z} = q \\ \end{aligned}\]

결과적으로 우리가 알고싶은 것은 input의 마지막 단에 대한 영향력이기 때문에, 위의 식들을 이용하여 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}$를 구할 것입니다.

이를 위해서 이제 역방향 전파(Backward Pass, Backpropagation)를 하게 됩니다. 즉, 오른쪽에서 왼쪽으로 가는 backward pass 를 구해야 위 세가지 값들을 구할 수 있습니다.

지금부터 오른쪽 끝에서 부터 하나씩 살펴보겠습니다.

오른쪽 끝으로 나가는 것이 $f$이기 때문에, 들어오게 되는 것은 자기자신을 미분을 한 결과인 $\frac{\partial f}{\partial f}$(i.e. identity function)가 되는데 이 값은 당연히 $1$이 됩니다.

다음으로, $\frac{\partial f}{\partial z}$를 구해보도록 하겠습니다. 이는 앞의 미분식에서 값을 구했듯이 $\frac{\partial f}{\partial z} = q$이기 때문에, 값은 q의 값인 3이 됩니다.

여기서 3이라는 값의 의미를 이해하고 넘어가야 하는데, $z$의 값을 $h$만큼 증가를 시키게 되면 $f$의 값은 $3h$만큼 증가하게 된다는 의미입니다. 즉 3배만큼 증가하게 된다는 뜻입니다.

다음으로, $\frac{\partial f}{\partial q}$를 구해야 되는데, 이 또한 앞에서 이미 구해놨습니다. 바로 $z$입니다. 그렇기 때문에 그 값은 $-4$가 됩니다. 여기서의 $-4$의 의미는 위에서 설명했었던 것과 같이, $q$의 값을 $h$만큼 증가시키게 되면 $f$는 $4h$의 값만큼 감소하게 된다는 의미입니다.

연쇄 법칙(Chain rule)

$\frac{\partial f}{\partial q}$ 까지 구했으니 이제 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}$의 값을 구해야 합니다. 그런데 이 값들은 따로 구해놓은 것이 없습니다.

따라서, 이떄 Chain rule을 이용해서 값을 구하게 되는데 연쇄법칙을 이용해서 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}$를 다시 쓰게 되면 다음과 같이 표현할 수 있습니다.

\[\begin{aligned} & \frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \times \frac{\partial q}{\partial x} \\ & \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} \times \frac{\partial q}{\partial y} \\ \end{aligned}\]

연쇄법칙을 통하게 되면, 우리가 미리 구해놓은 값들로 해당 값을 표현할 수 있기 때문에, 별다른 연산 없이 이미 알고 있는 값으로 우리가 알고싶은 값을 얻을 수 있습니다.

위의 식을 통해 각 값을 구해보게되면,

\[\begin{aligned} & \frac{\partial f}{\partial x} = z \times 1 = -4 \\ & \frac{\partial f}{\partial y} = z\times 1 = -4 \\ \end{aligned}\]

가 됩니다.

$\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \times \frac{\partial q}{\partial x}$에서 $\frac{\partial f}{\partial q}$는 $\frac{\partial f}{\partial x}$의 직접적인 gradient 값이 되기 때문에 이런 것을 local gradient라고 부르고, 반대로 $\frac{\partial q}{\partial x}$ 같은 경우를 global gradient라고 합니다.

Local gradient 와 Global gradient

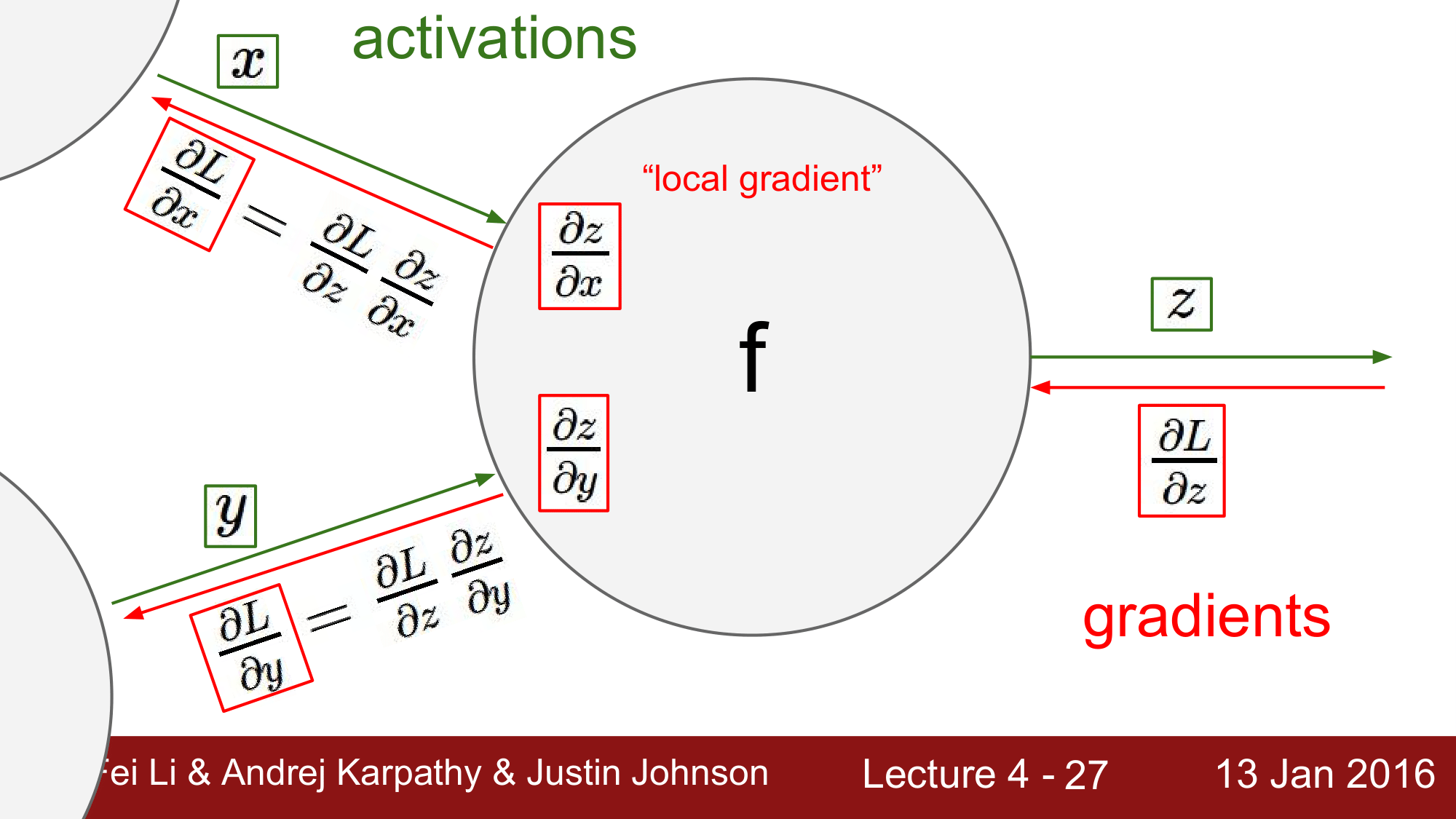
위 그림은 함수 $f$를 하나의 레이어 혹은 게이트로 하는 forward pass 과정을 나타낸 것 입니다.

이 과정에서, local gradient $\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}$ 값을 구할 수 있습니다.

앞에서 역전파 과정을 전개할 때 local gradient와 global gradient를 곱해준다고 설명한 바있는데, forward pass과정에서 이 local gradient를 바로 구할 수 있습니다. 이렇게 구하게 된 local gradient는 backpropagation전개 시에 사용해야 하기 때문에 메모리에 해당 값을 저장해둡니다.

global gradient는 뒷단에서 들어오는 값이기 때문에 backward pass를 하는 도중에만 값을 구할 수 있습니다.

정리하자면, local gradient는 forward pass시에 구하고, backward pass시에 global gradient를 계산하므로써 결과적으로 local gradinet와 global gradient를 곱해주어 gradient값을 얻을 수 있다는 것이 핵심이 되겠습니다.

즉, backward pass시에 최종적으로 chainning이 일어나게 된다고 할 수 있습니다. 따라서, $\frac{\partial L}{\partial x} = \frac{\partial L}{\partial z} \times \frac{\partial z}{\partial x}$ 가 되어 최종적으로 다음 레이어에 global gradinet값을 전달하게 됩니다. y부분의 역전파 값도 위와 같이 구할 수 있습니다.

이러한 과정을 Backward Pass = Backpropagation이라고 부릅니다.

이떄 뒤로 연결되어 있는 노드가 1개가 아니라 여러개의 노드가 연결되어 있으면, 그 각 노드로 부터 흘러들어오는 값의 합이 global gradient가 됩니다.

복잡한 역전파의 예

\[f(w, x) = \frac{1}{1 + \exp^{-(w_0x_0+w_1x_1+w_2)}}\]

총 5개의 입력을 갖고 있는 위의 함수를 Computational Graph로 표현하게 되면 다음과 같습니다.

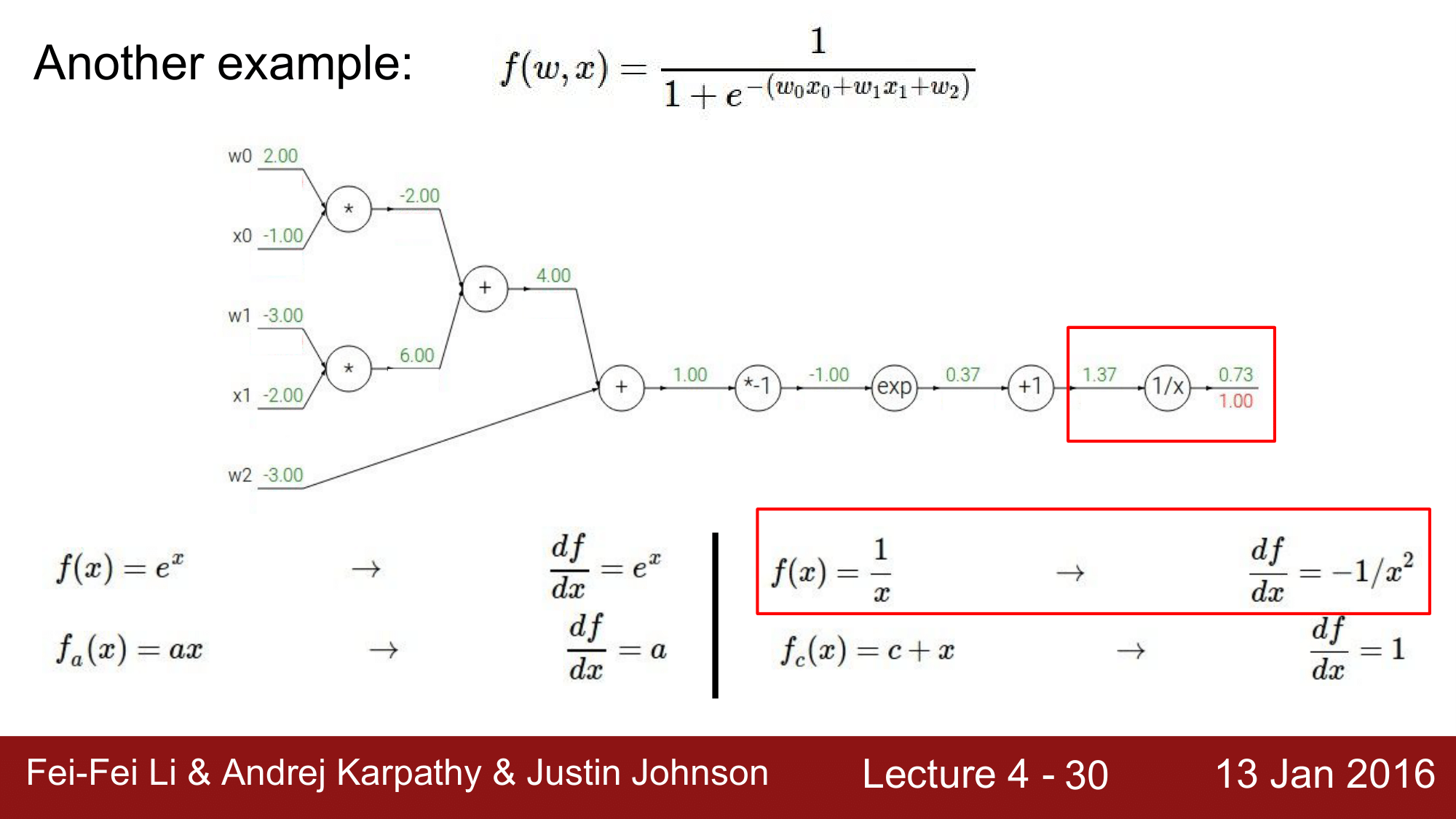
이 때, 오른쪽 끝을 $f$라고 한다면 다음의 값들을 구해야 합니다.

\[\frac{\partial f}{\partial w_0}, \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial w_1}, \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial w_2}\]

즉, 이들 각각이 최종적인 loss에 미치는 영향력을 구해보자는 것이 되겠습니다.

다음의 간단한 미분식들을 참고하여, 위의 값을 구해보도록 하겠습니다.

\[\begin{aligned} & f(x) = \exp^x \qquad \rightarrow \qquad \frac{df}{dx} = \exp^x \\ & f_a(x) = ax \qquad \rightarrow \qquad \frac{df}{dx} = a \\ & f(x) = \frac{1}{x} \qquad \rightarrow \qquad \frac{df}{dx} = -1/x^2 \\ & f_c(x) = c + x \qquad \rightarrow \qquad \frac{df}{dx} = 1 \end{aligned}\]

첫 번째로, 1/x 부분에서 좌측을 $da$ 우측을 $dL$이라고 한다면, 우리가 구해야 하는 것은 $\frac{dL}{da}$이기 때문에 $b$라는 것을 도입해서 Chain rule에 의해 이를 풀어 쓰게 되면 $\frac{dL}{da} = \frac{dL}{db} \times \frac{db}{da}$가 됩니다. 여기서 $\frac{db}{da}$는 local gradient이고, 이는 입력으로 들어온 1.37을 1/x에 대해 계산을 하면 되기 때문에, $\frac{-1}{1.37^2} = -0.53$이 됩니다. 그리고 global gradient는 $\frac{dL}{dL} = 1$이기 때문에 gradient를 구하게 되면 $1 \times -0.53 = -0.53$ 이 됩니다.

다음에도 위와 같은 방식으로 $dL = -0.53$, $da = 1$이기 때문에 $-0.53$이 됩니다.

exp 연산의 경우 $(e^{-1})(-0.53)$이 되므로 $-0.20$이 되고, *-1연산도 계산을 하게되면 $0.20$의 값을 얻게 됩니다.

$+$ 연산은 위의 $+1$ 때와 마찬가지로 $x + a$를 미분하게 되면 1이 되기 떄문에, local gradient는 $1$이 되고, global gradient는 뒤에서 들어온 값인 $0.20$이 되기 떄문에, 각각 $0.20, 0.20$이 됩니다.

$+$ 연산의 경우 보시다싶이 뒤에서 보내온 값을 앞으로 그대로 분배하여 흘려주기 때문에, gradient distributor라고도 불립니다.

그 다음에 또 $+$연산이 나오는데 이는 방금 설명했으니 넘어가도록 하겠습니다.

마지막으로 나오는 * 연산은 앞에서 설명했듯이 $\frac{\partial f}{\partial z} = q, \frac{\partial f}{\partial q} = z$로 위 아래 값을 바꿔주면 되기 때문에, $w_0$의 local gradient는 $-1.00$이 되고 $x_0$의 local gradient값은 $2.00$이 되겠습니다. 그래서 global gradient $0.20$과 함께 계산을 해보게 되면, 각각 $-0.20$, $0.40$이 되게 됩니다. 밑에 것도 마찬가지로 계산을 하여 정리하면 다음과 같습니다.

\[\frac{\partial f}{\partial w_0} = -0.20, \frac{\partial f}{\partial x_0} = 0.40, \frac{\partial f}{\partial w_1} = -0.40, \frac{\partial f}{\partial x_1} = -0.60, \frac{\partial f}{\partial w_2} = 0.20\]

시그모이드 함수(sigmoid function)

이렇게 5가지 입력에 대한 gradient를 모두 구했습니다. 앞에서 각 노드에서 미분을 하여 값을 앞으로 전달했으나, 1/x 부터 *-1까지의 노드를 한꺼번에 묶어 계산할 수도 있습니다. 이 부분을 sigmoid gate라 부르는데 바로 시그모이드 함수를 하나씩 풀어 쓴 노드들이기 때문입니다.

시그모이드 함수를 보면 다음과 같습니다.

\[\sum(x) = \frac{1}{1 + e^{-x}}\]

이는 앞에서 gradient를 구했던,

$f(w, x) = \frac{1}{1 + \exp^{-(w_0x_0+w_1x_1+w_2)}}$ 와 같은 모양임을 알 수 있습니다.

시그모이드 함수의 특징

시그모이드 함수는 미분을 하게 되었을 때 재미있는 특징을 가지고 있습니다.

미분을 하는 식을 보게 되면 다음과 같습니다.

\[\begin{aligned} \frac{d\sum(x)}{dx} = \frac{d}{dx} (1 + e^{-x})^{-1} \\ & = -1 \cdot (1 + e^{-x})^{-2} \cdot -e^{-x} \\ & = (1 + e^{-x})^{-2} \cdot e^{-x} \\ & = \frac{e^{-x}}{(1 + e^{-x})^2} \\ & = (\frac{1 + e^{-x} - 1}{1 + e^{-x}})(\frac{1}{1 + e^{-x}}) \\ & = (1 - \sum(x))\sum(x) \end{aligned}\]

결과적으로 $\frac{d\sum(x)}{dx} = (1 - \sum(x))\sum(x)$가 됩니다.

즉, 시그모이드 함수를 통과하게 되면 다른 값이 연산에 기여하지 않고 자기 자신만으로 값을 표현할 수 있는 대단한 특성을 갖고 있다는 것을 알 수 있습니다.

앞에서 복잡하게 계산했던 부분이 단 하나의 sigmoid gate 로 간단하게 표현됨으로써 손쉽게 값을 도출하게 되는 것 입니다.

역전파 흐름의 패턴

앞에서 잠깐씩 설명했던 Add Gate, Multiply Gate 등의 특징을 정리를 하게 되면 다음과 같습니다.

Add Gate: Gradient Distributor로 뒤에서 들어오는 값을 그대로 앞의 노드들로 분해해주는 특징을 갖습니다.
Multiply Gate: Gradient Switcher로 앞에서 들어오는 값을 위 아래로 바꿔 뒤에서 들어오는 값을 곱해 앞으로 흘려주게 됩니다.
Maximum Gate: Gradient Router로 앞으로 들어온 값중 큰 값으로만 뒤에서 들어온 값을 흘려주고, 작은 값은 0을 흘려주는 특징이 있습니다.

분기 그래프의 역전파

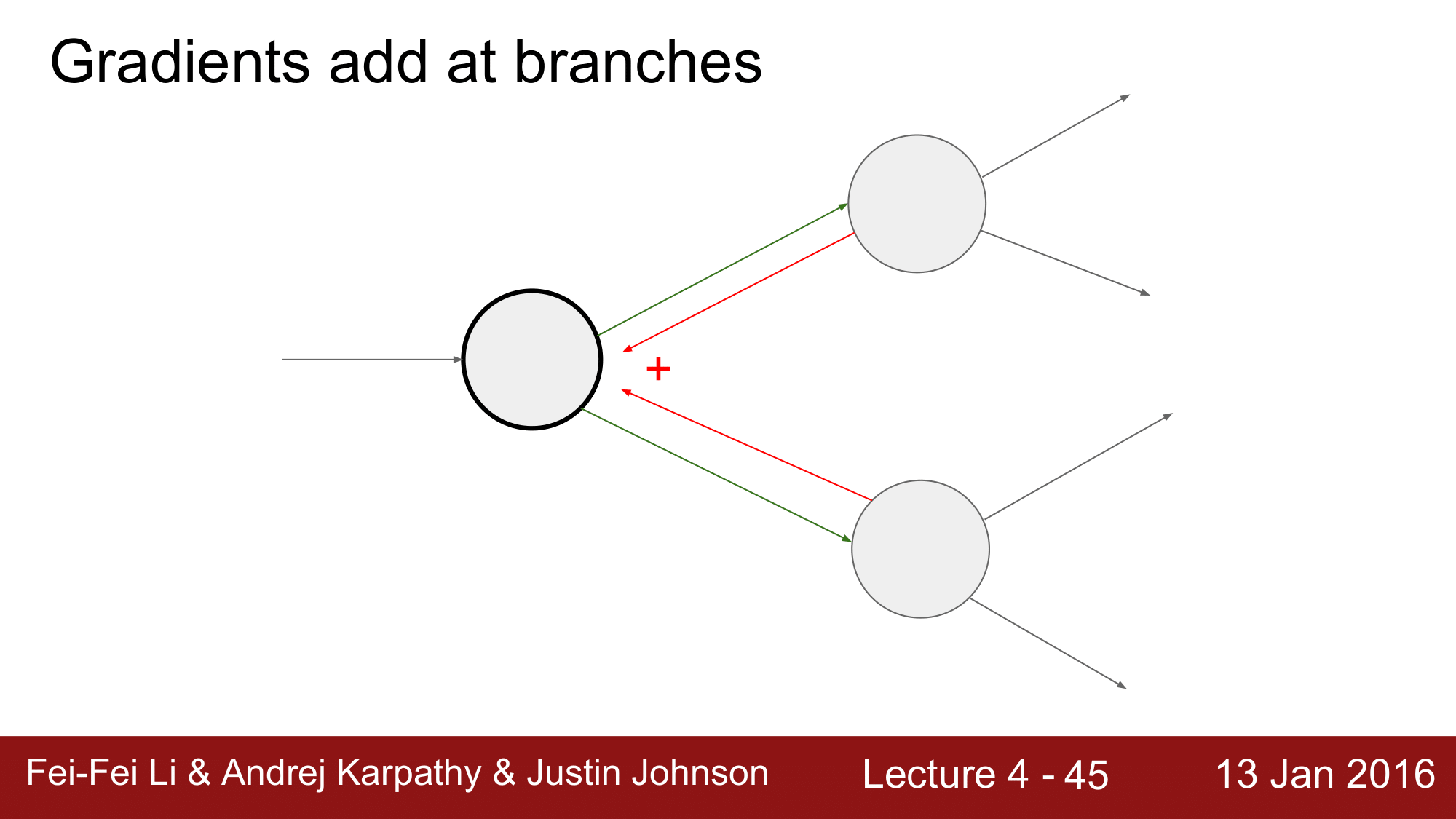
앞에서 잠깐 설명했던 내용인데, Backpropagation의 상황에서 뒷단이 여러개의 노드로 분기되어 있는 경우 입니다.

이 경우에는 여러개의 gradient들을 더해주면 된다는 것 입니다.

순전파와 역전파의 구현(Implementation of Forward and Backward)

지금까지 살펴보았던 Computational Graph를 코드로 구현하게 되면 다음과 같습니다.

class ComputationalGraph(object):
    # ...
    def forward(inputs):
        # 1. [pass inputs to input gates]
        # 2. forward the computational graph
        for gate in self.graph.nodes_topologically_sorted():
            gate.forward()
        return loss # the final gate in the grapo]h outputs the loss
    def backward():
        for gate in reversed(self.graph.nodes_topologically_sorted()):
            gate.backward() # little piece of backprop (chain rule applied)
        return inputs_gradients

순전파(forward)를 함수로 구현해서 들어오는 input들에 대해서 모두 순전파를 해준 뒤 loss를 return 하게 됩니다. 역전파(backward)의 경우에도 모든 게이트에 대해 역전파를 해준뒤 input들이 들어온 방향으로 global gradient를 return 하게 됩니다.

이 구현을 좀 더 자세한 코드로 살펴보겠습니다.

Multiply Gate

x, y, z가 scalar값이라고 할 때,

class MultiplyGate(obejct):
    def foward(x, y):
        z = x * y
        self.x = x  # must keep theese around!
        self.y = y
        return z
    def backward(dz):
        dx = self.y * dz    # [dz/dx * dL/dz]
        dy = self.x * dz    # [dz/dy * dL/dz]
        return [dx, dy]

앞에서 설명드렸던 것 처럼, forward pass를 할 때 이미 local gradient를 구할 수 있습니다. 이를 backpropagation시에 사용하여야 하기 때문에 해당 값을 객체 내에 저장을 해주고 backward pass가 진행될 때 local gradient값을 꺼내어 들어온 global gradient와 곱해 gradient값을 반환할 수 있도록 위와 같이 구현합니다.

백터에서의 기울기 연산(Gradients for vectorized code)

이제 앞에서 설명했던 연산을 현실적으로 활용할 수 있도록, gradient를 구할 때 x, y, z가 scalar 가 아닌 vector라고 하면 어떻게 되는지 생각해보겠습니다.

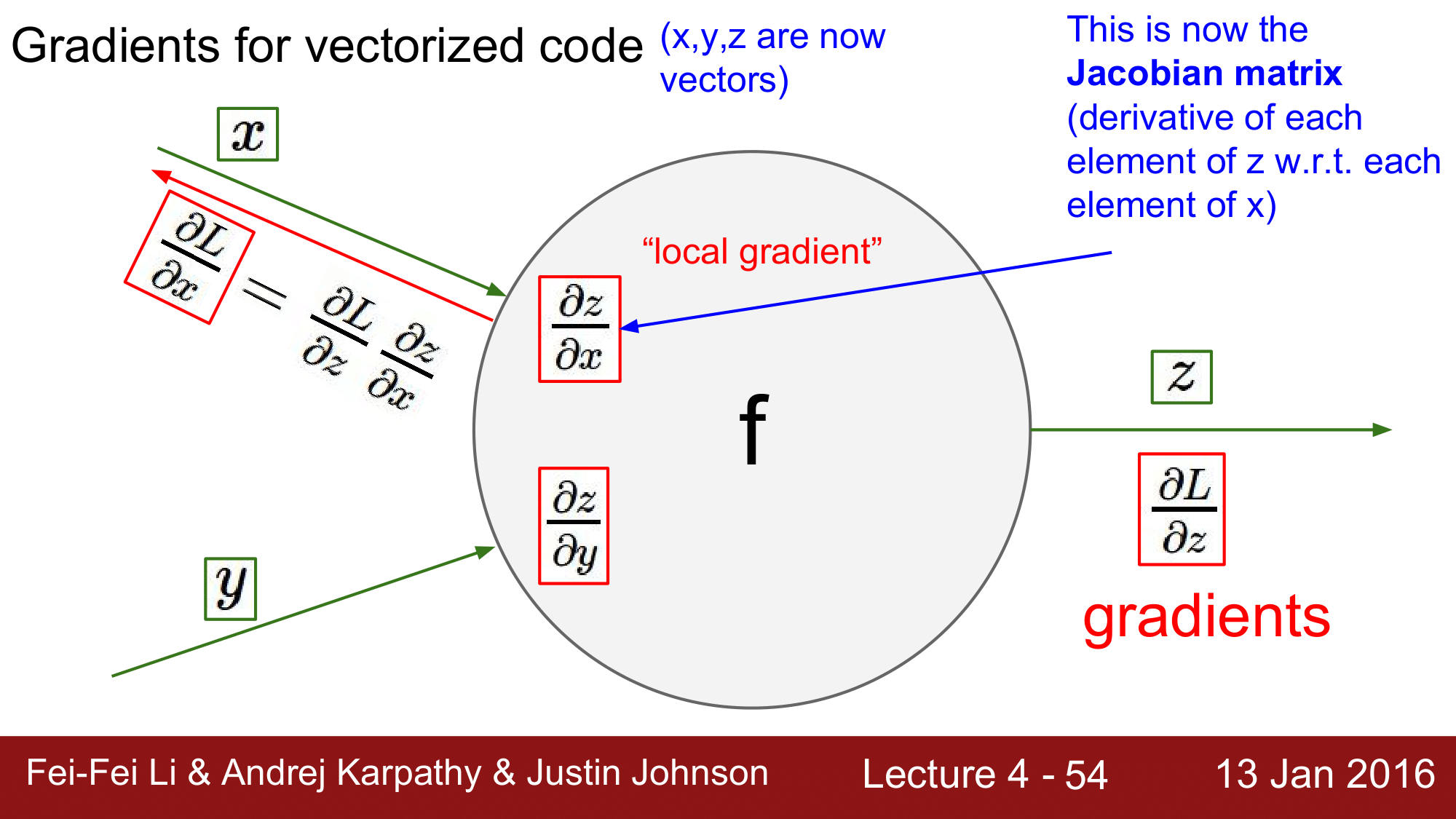
그렇게 되면, $\frac{\partial L}{\partial x} = \frac{\partial L}{\partial z} \frac{\partial z}{\partial x}$ 에서 $\frac{\partial L}{\partial z}$는 vector가 되고, $\frac{\partial z}{\partial x}$는 Jacobian matrix가 되게 됩니다.

여기서, 이제 vectorized operation이 일어나게 되어

미니배치가 적용된 기울기

요약

신경망은 매우 크기 때문에, 모든 변수들에 대해 일일히 Gradient Formula를 기록할 희망은 없다.
Backpropagation은 모든 inputs, parameters, intermediates의 gradient 계산을 위해 Computational Graph에 Chain rule을 반복적으로 적용한다.
노드가 forward(), backwward() API를 구현하는 그래프 구조를 유지한다.
순전파(forward): 연산의 결과를 계산하고,gradient계산에 필요한 모든 중간 변수들을 메모리에 저장한다.
역전파(backward): 입력에 대한 loss function의 gradient를 계산하기 위해 chain rule을 적용한다.

2. 신경망(Neural Network)

지금까지 Linear Score function을 구할 때는 $f = Wx$라고 간단하게 표현했습니다만, 이제 신경망에서 2-layer Neural Network가 된다면 $f = W_2max(0, W_1x)$ 처럼 표현하게 됩니다.

여기에서 $max$의 경우, activation function 중 하나인 Relu인데 이 활성화 함수(activation function)의 여러가지 종류에 대해서는 뒤에서 자세히 설명하겠습니다. 간단하게만 설명드리자면, 여기에서는 activation function의 경우 비선형적(Non Linearity)이라는 것만 알아두면 될 것 같습니다.

이런 신경망에서는 다음과 같은 구조로 전개되는데,

위 그림은 input이 3072개가 들어오고 W1을 거쳐 100개의 노드로 구성된 h(hidden layer)가 된 후 W2를 적용하여 s는 10개의 클래스로 분류한다는 것을 도식화 한 것입니다.

이때, Data-Driven Approach에서의 Nearest Neighbor의 한계가 무엇이었는지를 생각해보면 위와 같이 구성된 신경망의 이점에 대해 잘 느낄 수 있습니다.

Data-Driven Approach에서의 Nearest Neighbor는 object들이 갖는 특징(색상, 방향 형태 등)들을 하나로 merge한다고 했었는데, merge를 하는 이유는 각각의 클래스에는 단 하나의 Classifier가 존재하기 떄문에 그렇습니다.

예를들어, 자동차를 인식해내는 Classifier는 다른 색상의 자동차가 있음에도 불구하고 빨간색만 분류를 한다는 것이 있었고, 말의 경우에도 왼쪽을 보는 말에 더 특화되어 인식하게되는 이러한 특징이 있었습니다.

하지만 신경망에서는 은닉층에 있는 100개의 노드들 각각이 하나의 feature를 담당합니다. 즉, 한개의 클래스에 대해 하나의 Classifier만을 갖는 Non parametric Approach와 다르게 CNN과 같은 Parametric Approach는 은닉층 내의 여러 노드들이 각각 Classifier가 되어, 결과적으로 하나의 클래스에 여러개의 Classifier를 갖게 되는 것입니다.

위의 설명에서 은닉층을 100개의 노드로 구성한다고 했었는데, 여기서의 100개는 설명을 위해 임의로 설정한 값이고, 실제로는 노드의 개수 같은 경우 하이퍼파라미터로 실험을 통해 최적의 값을 구해 학습을 진행하여야 합니다.

2계층 신경망의 구현(Implementaion of 2-layer Neural Network)

다음 코드는 @imtrask에서 가져온 코드로 2계층 신경망에 대해 작성한 코드입니다.

X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
# 1이 2개이기 때문에, binary classification 
Y = np.array([0,1,0,0]).T

# Weight(Synaps)를 표현해주는 것
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
    # Sigmoid 적용
    l1 = 1/(1+np.exp(-(np.dot(X, syn0))))
    l1 = 1/(1+np.exp(-(np.dot(l1, syn1))))
    # Backpropagation
    l2_delta = (y - l2) * (l2 * (1 - l2))
    l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
    # Parameter update
    syn1 += l1.T.dot(l2_delta)
    syn0 += X.T.dot(l1_delta)

생물학적 뉴런과 인공 뉴런(Biological Neuron and Artificial Neuron)

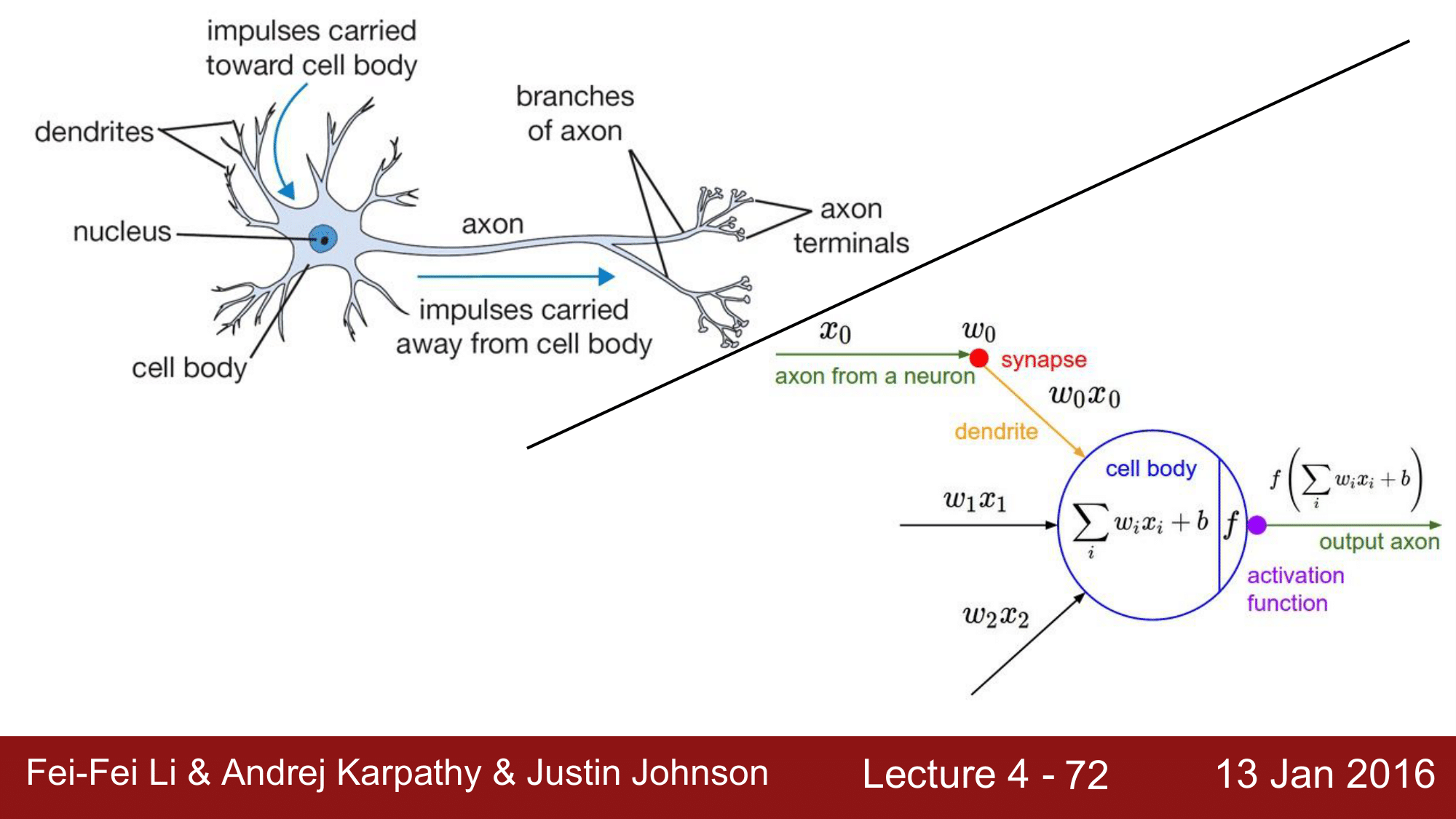
위 그림에서 보면, Biological Neuron의 경우 cell body(soma)라는 부분과, 입력이 들어오는 dentrites라는 부분, 연산결과를 output으로 내보내기 위한 axon이라는 부분으로 이루어져 있습니다. 이런 하나의 뉴런이 여러개가 연결이 되면서 전달과정이 반복해서 이루어지는 것인데, 이를 그래프로 단순화 하면 오른쪽 그림과 같게 됩니다.

$x_0$이라는 데이터가 들어와서 $w_0$이라는 synapse 가중치와 연산을 하고 이것들이 모여서 cell body 내에서 단순한 합 연산이 이루어지게 됩니다. 이렇게 해서 나온 결과를 activation function을 적용을 해서 Non Linearity를 만들어주고, 이것을 axon을 통해 다음 뉴런으로 전달하게 되는 과정이 되겠습니다. 물론 여기서 $w_0, w_1, w_2$의 가중치들이 각각의 dendrite를 통해서 들어온 데이터들에 대해 얼마나 영향을 줄 것인가를 결정하게 될 것입니다.

activation function 들 중에 전통적으로 많은 사랑을 받아왔던 것은 바로 시그모이드 함수(Sigmoid Function입니다. 그 이유는, 그래프를 보면 알 수 있습니다.

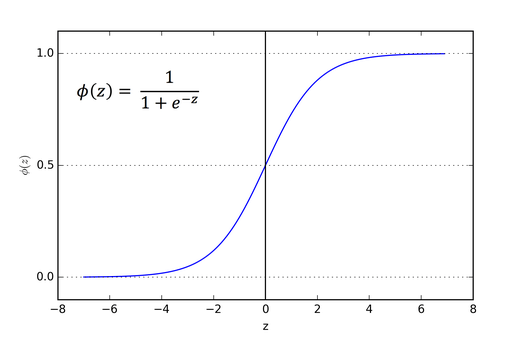
그래프를 보게 되면, x가 0일 때 0.5의 값을 가지면서 x가 아무리 작아져도 0 이상이 되고 x가 아무리 커진다 한들 1이하가 됩니다. 즉, 어떤 뉴런의 영향력을 0과 1사이의 값으로 확률처럼 특정해주기가 쉽기 때문입니다.

이것을 코드로 표현을 하게 되면 다음과 같습니다.

class Neuron:
    # ...
    def neuron_tick(inputs):
        """ assume inputs and weights are 1-D numpy arrays and bias is a number """
        cell_body_sum = np.sum(inputs * self.weights) + self.bias
        firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum))    # sigmoid activation function
        return firing_rate

input 값으로 vector를 받아서 cell_body_sum에서 단순 sumation을 히고, 아래 행에서 sigmoid 함수에 적용시켜 Non Linearity를 만들어주고 이 값을 반환해 주어 다음 뉴런으로 값이 전달되도록 하는 코드입니다.

여기에서 주의해서 봐야할 점은, 인공신경망이 우리의 실제 두뇌와 유사하다고는 하지만 생물학적인 뉴런은 인공신경망에 비해 훨씬 더 다양한 종류가 있고, dendrite에서 훨씬 더 복잡한 non-linear 연산을 수행하며, 시냅스 역시 단 하나의 가중치만으로 이루어진 것이 아니라 복잡한 비선형 동적 시스템이라는 것입니다.

그래서 인공신경망을 너무 우리 신경망에 매칭시켜서 보는 것에 대해 주의가 필요합니다.

활성화 함수(Activation Functions)

활성화 함수에는 다양한 것들이 존재하는데, 유명한 몇개의 함수들을 소개하자면 다음과 같습니다.

Sigmoid $\sum(x) = 1/(1 + e^{-x})$

tanh $tanh(x)$

ReLU $max(0, x)$

ReLU는 현재 가장 많이쓰고 있는 활성화함수로 0과 x에 대해 max를 취하는 형태로 되어 있습니다. 물론, ReLU도 개선사항이 많지만 기장 기본으로 사용하고 있습니다.

Leaky ReLU $max(0.1x, x)$

위에서 언급했던, ReLU의 개선사항을 적용한 함수로, 이와 같은 다양한 변형들이 존재합니다. 이외에도 다음과 같은 변형 함수들이 존재합니다.

Maxout $max(w_1^Tx + b_1, w_2^Tx + b_2)$

ELU

$f(x) = \begin{cases} x \qquad \text{if}\ x > 0
\alpha (\exp(x)-1) \end{cases}$

신경망의 구조(Architectures of Neural Network)

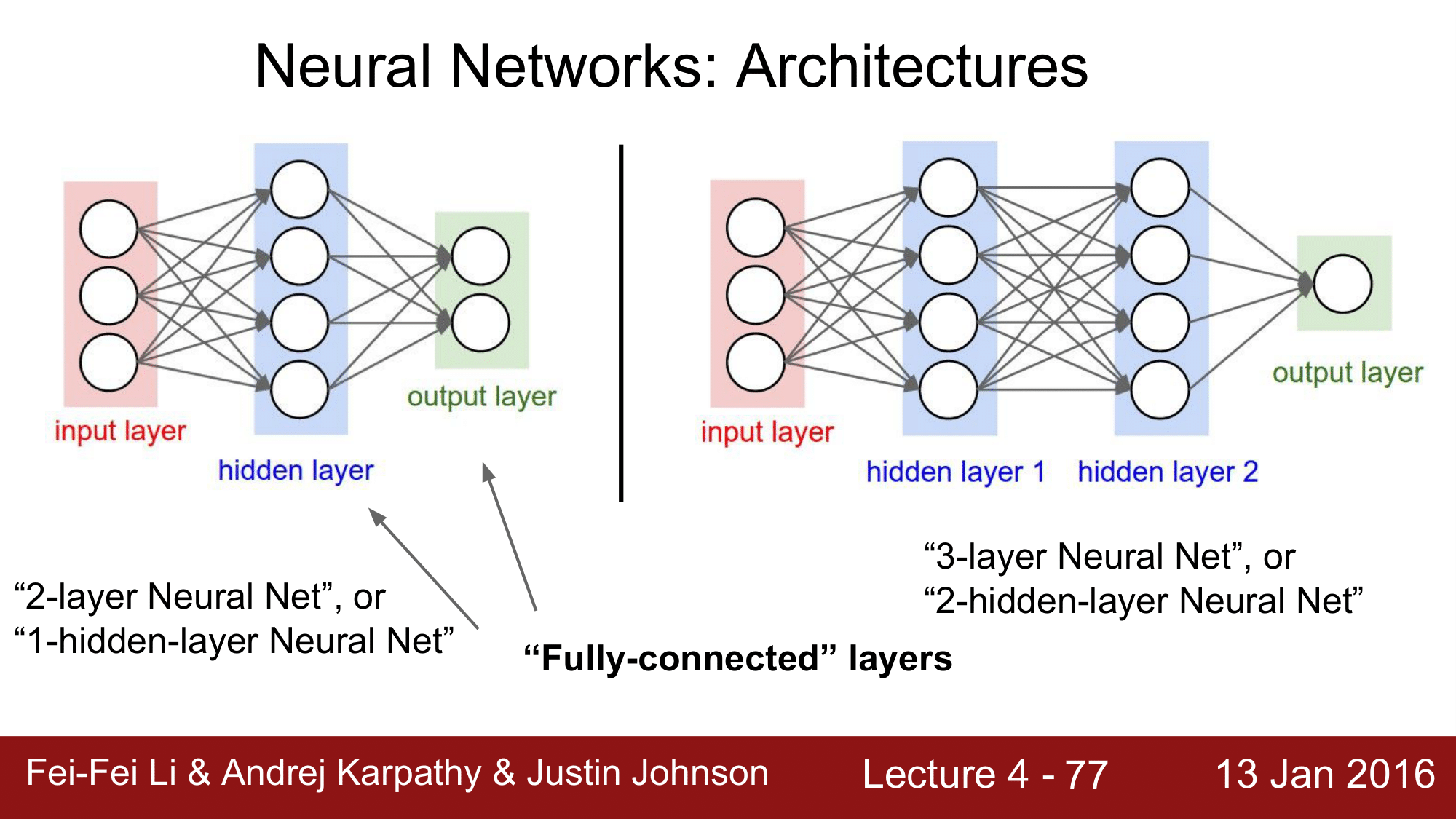
신경망의 경우 위 그림과 같은 구조로 구성이 되는데, 왼쪽의 신경망의 경우 2-layer Net 혹은 1-hidden-layer Net이라고 부릅니다.

layer 가 보기에는 3개인데 왜 2-layer라고 부르는지에 대해 의문을 갖을 수 있는데, 이는 기본적으로 가중치(wegiht)를 가지고 있는 것들을 레이어(layer)라고 부르기 때문에 input Layer를 제외하게 되어 2-layer 라고 부릅니다. 오른쪽에 있는 신경망 또한 같은 이유로 3-layer 신경망이라고 부릅니다.

그리고 각각의 레이어들은 각 레이어 내에 모든 노드들이 화살표로 연결되어 있는 것을 볼 수 있는데, 이렇게 모든 노드들이 연결되어 있는 레이어들을 완전연결(Fully-connected; FC) layers라고 부릅니다.

이렇게 layer 로 신경망을 구현하고 FC로 연결하는 이유는 이를 통해 효율적으로 계산을 할 수 있기 때문입니다.

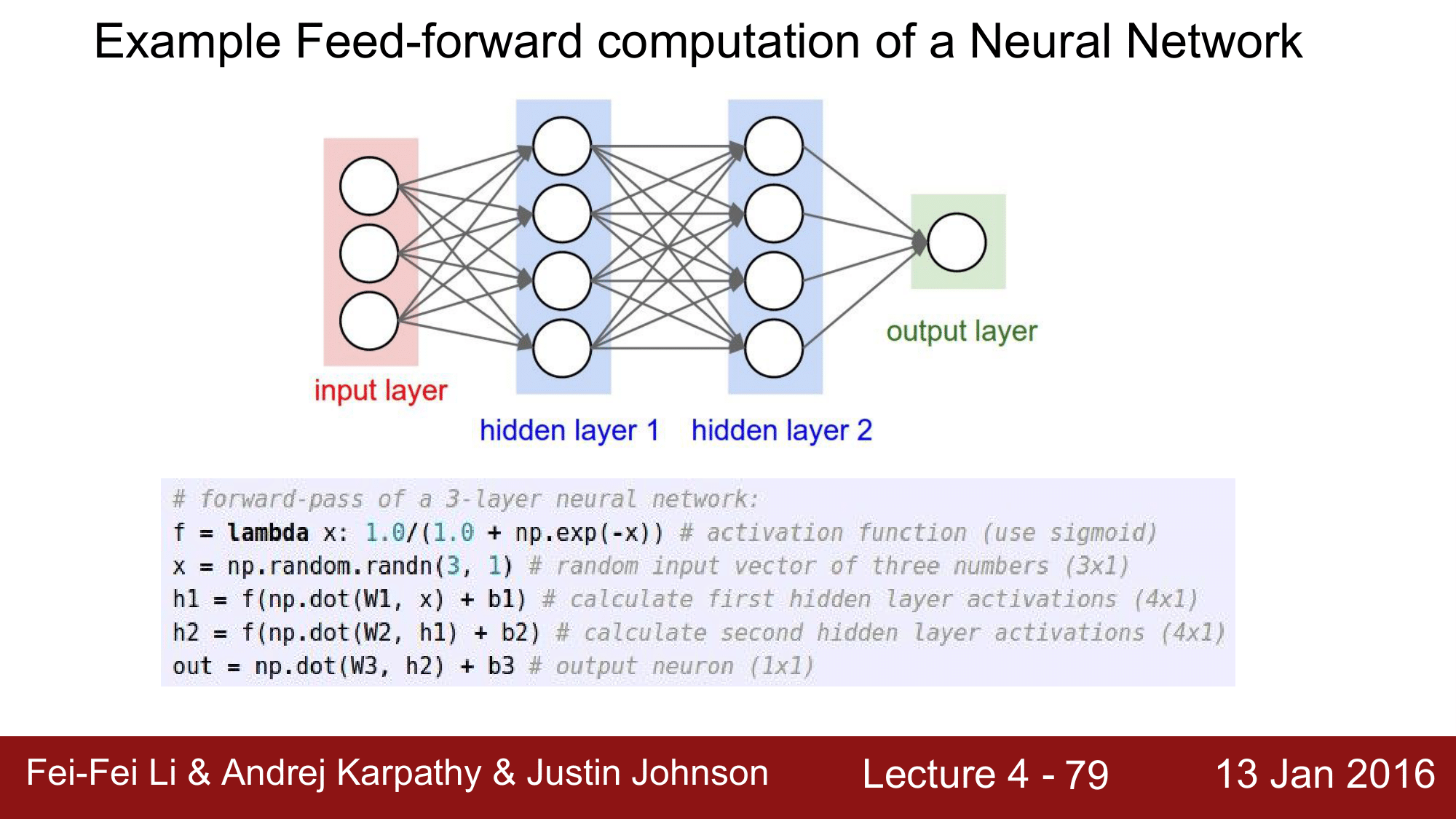
위와 같이 FC로 레이어들이 연결되어 있으면 vertorized operation을 가능하게 해서 다음 코드와 같이 구현이 쉽게 되는 것을 알 수있습니다.

# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x))    # activation function (use sigmoid)
x = np.random.randn(3, 1)   # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1)  # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3   # output neuron (1x1)

뉴런 개수에 따른 분류의 차이

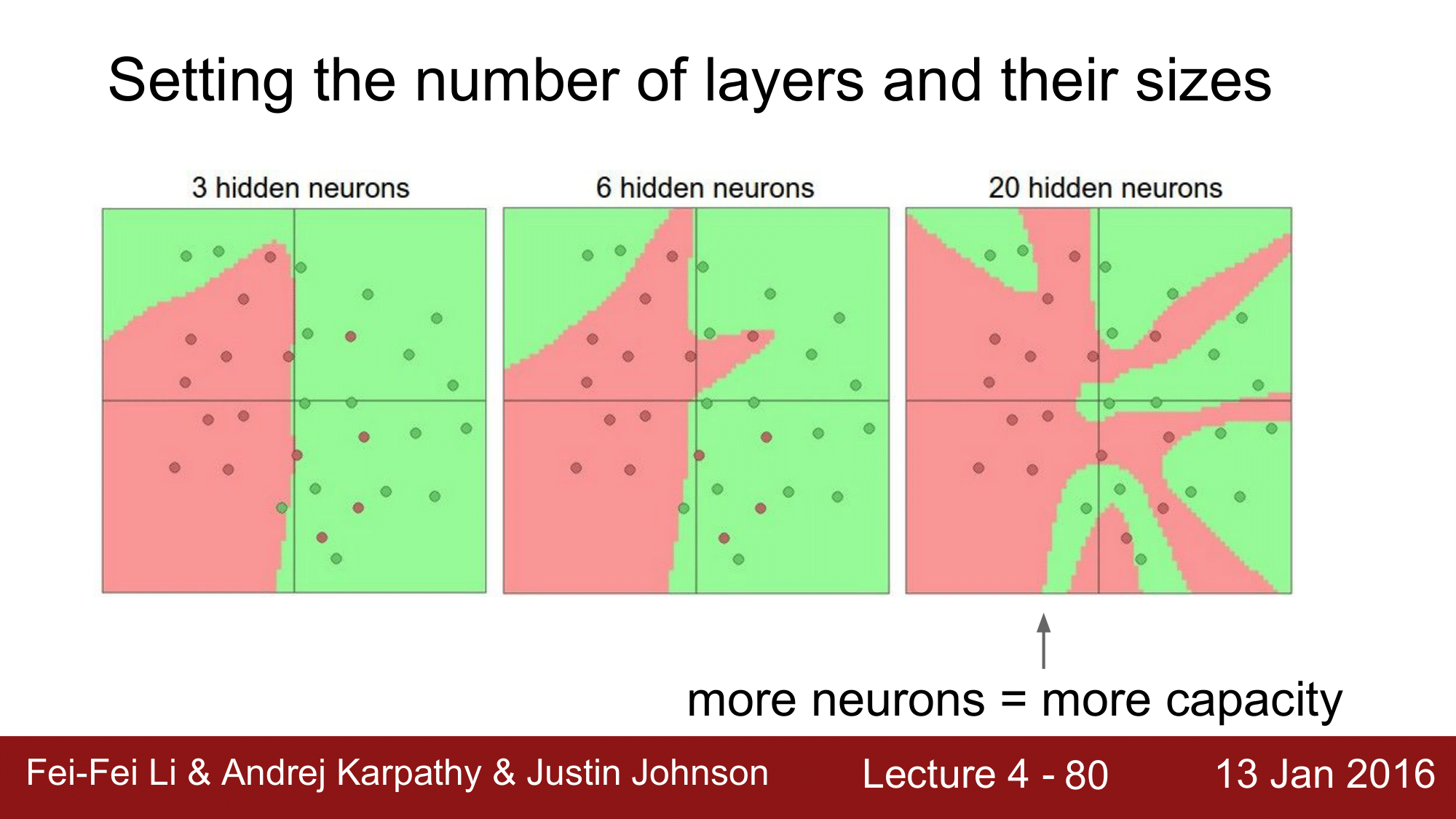
위의 예시는, 레이어의 개수에 따라 분류능력이 좋아지는 것을 보여주는데, 여기서 조심해야 할 점은 Neural Net의 사이즈가 Regularization의 역할을 하는 것이 아니라는 것 입니다.

일반화를 하기 위해서는 Regularization Strength를 높혀야 하는 것 입니다. $\lambda = 0.001$ 일 때와 $\lambda = 0.1$일 때를 비교해서 보게되면, $\lambda = 0.1$일 때가 훨씬 더 일반화가 된다는 것을 확인할 수 있습니다. 즉, training data에 오버피팅(overfitting)되지 않으면서, test data 에 좀 더 일반화 시키는 효과를 볼 수 있다는 것입니다.

그래서 정리를 하자면, Data에 오버피팅이 일어나지 않도록 Neural Network을 잘 구성하는 방법은 Network 을 작게 만드는 것이 아니고, Regularization Strength를 더 높여주어야 한다는 점입니다.

따라서 Neural Network 는 Regularization을 잘 한다는 전제하에 더 크면 클수록 좋다는 것 입니다.

요약

뉴런을 완전연결계층(Fully-connected layers)로 배열한다.
추상화 계층은 효율적인 vectorized code(e.g. matrix multipies)를 사용할 수 있는 좋은 속성을 가지고 있다.
신경망(Neural Network)는 실제 신경이 아니다.
신경망(Neural Network)는 클수록 좋은 성능을 내지만, Regularization이 강하게 동반되어야 한다.

Share: Twitter, Facebook