Lecture 3. 손실함수와 최적화(Loss functions and Optimization)

해인 · October 21, 2020

CS231n

해당 포스트는 송교석 님의 유튜브 강의를 정리한 내용입니다. 강의 영상은 여기에서 보실 수 있습니다.

Recall from last time

Challenages in Visual Recognition

  • Camera pose
  • Illumination
  • Deformation
  • Occlusion
  • Background clutter
  • Intraclass variation

데이터 기반 접근 방식(Data-Driven Approach)

  • KNN(k-Nearest Neighbor)

Parametric Approach

  • Linear Classifier

선형분류의 경우 두가지의 해석 방법이 존재하는데 이는 다음과 같다.

  • 템플릿들을 매치해가는 과정 (i.e. Matching Template)
  • 고차원 공간에 있는 이미지들 사이에서 클래스 Score를 기반으로 구분을 해 나가는 과정

TODO

  1. Loss function: Score에 대해 불만족하는 정도를 정량화 하는 손실함수(Loss function)에 대한 정의
  2. Optimization: 손실함수를 최소화 하는 parameter를 효율적으로 찾는 방법

1. 손실 함수 (Loss function)

손실함수에는 다양한 함수들이 존재하는데 여기에서는 다음 두가지 함수에 대해 알아보도록 하자.

  • SVM - Hinge Loss
  • Softmax - Cross entorpy loss

SVM - Hinge Loss

$x_i$ 가 이미지이고 $y_i$ 가 (정수형) 레이블일 때, score vector를 $s = f(x_i, W)$ 로 나타낼 수 있고 SVM loss 는 아래 식과 같은 형태로 나타낼 수 았다.

\[L_i = \sum_{j \ne y_i} max(0, s_j - s_{y_i} + 1)\]

위 식을 살펴보면, max 함수 이기 떄문에 0과 $s_j - s_{y_i} + 1$ 중 큰 값을 반환한다는 의미이고, $s_j$는 잘못된 label의 스코어, $s_{y_j}$는 제대로된 label의 스코어이다. 그리고 뒤의 1은 safety margin이라고 한다.

이때 $s_j - s_{y_i} + 1$ 를 변형하면 $s_j - (s_{y_i} - 1)$가 되는데 이는 정답 레이블에서 1을 뺀 값이 잘못된 레이블의 스코어보다 작으면 0을 반환하고 이 보다 크면 해당 값을 반환하게 된다는 의미이다.

예를 들어, 고양이 이미지 class에 대한 값을 넣어 식을 살펴보면 다음과 같다.

\[\begin{aligned} &max(0, 5.1 - 3.2 + 1) + max(0, -1.7 -3.2 + 1) \\ &= max(0, 2.9) + max(0, -3.9) \\ &= 2.9 + 0 \\ &= 2.9 \end{aligned}\]

SVM loss 에서 $j = y_i$ 인 경우를 제외하여 계산하고 있는데, 이 경우를 포함하여 계산하게 되면 어떻게 될까? $j = y_i$이면 $s_j = s_{y_i}$이기 때문에 결과적으로는 $\sum$ 한 값이 모두 $+1$ 이 되어버리기 때문에 그 평균값인 최종 loss 값도 $+1$인 값이 될 것이다.

그리고 우리가 트레이닝 할 때 W값을 보통 0과 가까운 값(i.e. $s ~= 0$)을 주고 시작을 하게 되는데, 이 때의 Loss 값을 구해보면 위의 예에서는 2가 나옴을 알 수 있다. 즉, 처음 트레이닝 시에는 항상 Class의 개수 - 1의 값을 갖게 되는데 이를 이용하여 연산이 잘 되고 있음을 확인하는 것을 Sanity Check 라고 한다.

SVM loss 를 numpy code 로 보게 되면 다음과 같다.

\[L_i = \sum_{j\ne y_i} max(0, s_j - s_{y_i} + 1)\] 
def L_i_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0  # $j = y_i$인 경우에 대한 처리
    loss_i = np.sum(margins)
    return loss_i

여기에서 x 는 image single color vector 를, y는 lable을 나타내는 integer값을, W는 파라미터인 Weight Matrix를 의미한다.

이를 다시 수식으로 나타내게 되면 다음과 같다.

\[f(x, W) = Wx\] \[L = \frac{1}{N}\sum_{i=1}^{N} max(0, f(x_i; W)_j - f(x_i; W)_{y_j} + 1)\]

하지만 위 수식에는 버그가 존재한다. 만약 $L = 0$ 이 되는 $W$를 발견했다고 했을 떄 이 $W$값이 unique 하지 않다는 것이다.

다음 식을 한번 봐보도록 하자.

\[\begin{aligned} \\ &max(0, 1.3 - 4.9 + 1) + max(0, 2.0 - 4.9 + 1) \\ &= max(0, -2.6) + max(0, -1.9) \\ &= 0 + 0 \\ &= 0 \end{aligned}\]

위의 W값을 2배 했을 때,

\[\begin{aligned} \\ &max(0, 1.3 - 9.8 + 1) + max(0, 2.0 - 9.8 + 1) \\ &= max(0, -6.2) + max(0, -4.8) \\ &= 0 + 0 \\ &= 0 \end{aligned}\]

위의 두 식을 보게 되면 W값이 다름에도 불구하고 $L = 0$이 됨을 알 수 있다.

이런 문제점 때문에 unique 한 W값을 만들기 위해 Regularization strength 라는 lamda 값(hyperparameter)을 도입합니다.

\[L = \frac{1}{N}\sum_{i=1}^{N} max(0, f(x_i; W)_j - f(x_i; W)_{y_j} + 1) + \lambda R(W)\]

$\lambda R(W)$ 값은 W가 얼마나 괜찮은가에 대한 정도를 측정하는 역할을 수행합니다.

좌측항 $\frac{1}{N}\sum_{i=1}^{N} max(…)$ 을 data loss라고 하는데 이 부분은 학습용 데이터를 최대한 최적화하기 위한 수식이고, regularization loss라고 하는 우측항 $\lambda R(W)$은 테스트 셋에 최대한 일반화를 하기 위한 수식이다.

이렇게 좌측항과 우측항이 서로 값을 조정하면서 데이터에 가장 최적화 되고 가장 작은 W값을 추출하게 되는 것이다. regularization loss의 값에 의해 트레이닝 시에 에러가 커질 수 있지만; 즉 정확도가 낮아질 수 있지만, 우리가 더 중요시하고 있는 테스트에 대한 performance는 더 좋아질 수 있다.

또 다른 관점에서는 regularization loss입장에서는 W가 0이 되길 원하고 data loss에서는 W가 0이 될 수는 없기 때문에 서로 값을 조정하면서 더 좋은 W 값을 도출해 낼 수 있다.

regularization loss로 보통 다음과 같은 것들을 사용한다.

  • L2 regularization
  • L1 regularization
  • Elastic net (L1 + L2)
  • Max norm regularization
  • Dropout

L2 regularization의 동기

\[x = [1, 1, 1, 1]\\ w_1 = [1, 0, 0, 0]\\ w_2 = [0.25, 0.25, 0.25, 0.25]\] \[w_{1}^{T}x = w_{2}^{T}x = 1\]

위 식에 대해서 loss 를 계산하게 되면 $w_1, w_2$ 에 대한 결과가 모두 1이 되는데 regularization에서는 $w_2$ 의 값을 더 선호한다.(i.e. diffuse over everything)

이에 대한 해석은 다음과 같다.

$w_2$의 경우 $x$에 대해 모든 값에 영향을 주는 반면, $w_1$의 경우 하나의 값에만 영향을 주게 되는데, Regularization의 경우 weight 를 최대한 spread out 해서 모든 input feature 들을 고려하길 윈하기 때문이다.

Softmax Classifier (Multinomial Logistic Regression)

Softmax Classifier란 이항에 대한 Logistic Regression을 다차원으로 일반화 한 것이라고 할 수 있다.

여기서 scores 는 클래스를 log 화 한 확률 (not normalized)을 나타내고 이를 식으로 표현하면 다음과 같다.

\[P(Y = k|X = x_i) = \frac{e^sk}{\sum_j e^sj} \quad where\quad s = f(x_i \cdot W)\]

이때, $\frac{e^sk}{\sum_j e^sj}$를 Softmax function이라고 한다.

근데 여기서 하고자 하는 것은 클래스에 대한 $-log$ 의 확률을 최대화 하는 것이기 때문에 위의 식은 아래와 같이 쓸 수 있으며

\[L_i = -log P(Y = y_iu|X = x_i)\]

이를 정리하면 다음과 같아지는데, 이 아래의 수식을 cross entropy loss라고 부른다.

\[L_i = -log(\frac{e^sy_i}{\sum_j e^sj})\]

Softmax 에서는 $-log(x)$ 의 형태로 식이 전개 되는데 이를 형태를 그래프로 보게 되면

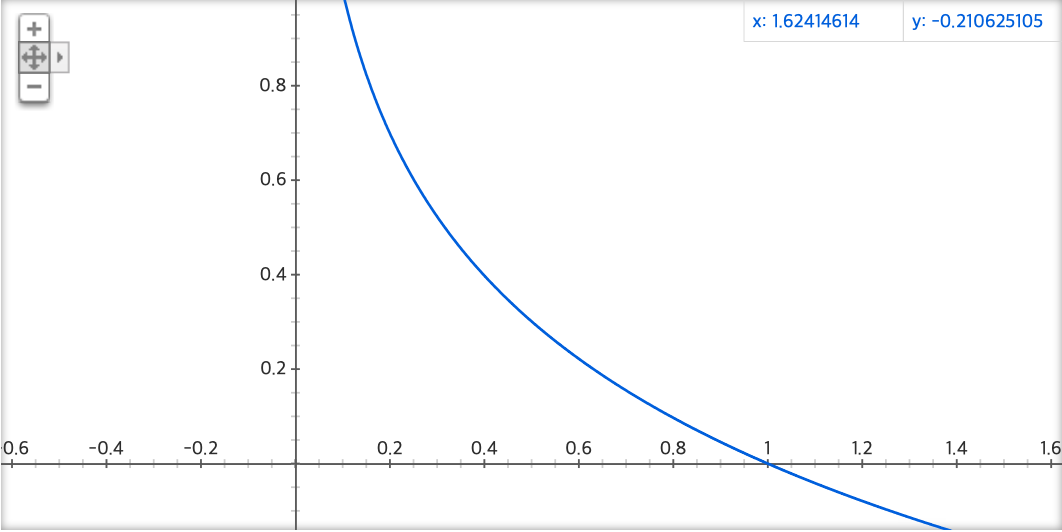
위와 같이 되는데 Softmax Loss는 확률이기 때문에 $0\le x \le 1$의 범위를 갖게되고, 때문에 최대 최소의 범위는 $0 \le y < \infty$ 이 된다.

이전에 살펴봤던 SVM에서는 sanity check 값이 “클래스 개수 - 1”이 었었는데 Softmax 에서는 위의 수식에 0을 넣어보면 알 수 있듯이, $\frac{1}{number\ of\ class}$가 됨을 알 수 있다.

Softmax vs, SVM

그럼 Softmax 와 SVM을 비교해보자.

\[L_i = -log(\frac{e^sy_i}{\sum_j e^sj})\qquad L_i = \sum_{j\ne y_i} max(0, s_j - s_{y_i} + 1)\]

현업에서는 Softmax가 SVM에 비해 더 많이 사용되는데 그 이유는 SVM의 경우 수식 뒷부분에 $+1$를 해주는 safety margin이 존재해서 이 값 때문에 데이터의 변화에 대해 둔감한 반면, Softmax의 경우 safety margin과 같은 인자값이 존재하지 않아 데이터 변화에 대해 더 민감하게 반응할 수 있기 때문에 그렇다.

2. 최적화(Optimization)

Optimization이란 기본적으로 loss 를 minimize 하는 weight를 찾아가는 과정이라고 생각을 하면 된다.

Recap

앞의 내용을 다시 한번 정리해보면 다음과 같다.

  • $(x, y)$에 대한 dataset
  • score function 이 $s = f(x; W) =^{e.g.} Wx$
  • loss function
    • Softmax: $L_i = -log(\frac{e^sy_i}{\sum_j e^sj})$
    • SVM: $\sum_{j\ne y} max(0, s_j - s_{y_j} + 1)$
    • Full loss: $L = \frac{1}{N}\sum_{i=1}^N L_i + R(W)$

Full loss 에서 Regularization function는 데이터에 영향을 받는 함수가 아니라 W(Weight)에 영향을 받는 함수 라는 점을 기억해두자.

최적화 전략(Optimization Strategy)

다시 본론으로 돌아와서 최적화를 위한 전략에는 Random Search와 Follow the slope 가 있는데 하나씩 살펴보도록 하자.

랜덤 서치는 최적화 전략 중 하나이긴 하지만 절대로 사용하면 안되는 전략인데, 이에 대한 코드를 보며 설명해보도록 하겠다.

# assume X_train is tthe data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are the labels (e.g. ID array of 50,000)
# assume the function L evaluates the loss function

bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
    W = np.random.randn(10, 3073) * 0.0001  # generate random parameters
    loss = L(X_train, Y_train, W)   # get the loss over the entire training set
    if loss < bestloss: # keep track of the best solution
        bestloss = loss
        bestW = W
    print ('in attempt %d the loss was %f, best %f' % (num, loss, bestloss))

# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (truncated: continues for 1000 lines)

위와 같이 1000 회를 반복해서 예측을 하게 되는데

결과를 보면 다음과 같이 15.5%의 정확도를 얻어, SOTA(state of the art) 즉 최고기록은 95% 정도임을 알 수 있다.

# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols)    # 10 x 10000, the class scores for all test examples
Yte_predict = np.argmax(scores, axis=0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_predict == Yte)
# returns 0.1555

Optimization을 해 나가는 과정은 산속에서 눈을 가리고 가장 낮은 곳을 찾아가는 과정이라고 할 수 있는데, random search의 경우 여기 저기 순간이동을 하면서 가장 낮은 곳을 찾는 방법이기 때문에 좋은 방법이라고 할 수 없다는 것을 알 수 있습니다.

그렇기 때문에 실질적으로 random search를 사용하지 않고 다음으로 소개하는 follow the slope 전략을 사용합니다.

Strategy #2. Follow the slope

follow the slope 전략은 경사를 따라가는 전략으로 1차원의 경우의 식은 다음과 같습니다.

\[\frac{df(x)}{dx} = \lim_{h\rightarrow0} \frac{f(x + h) - f(x)}{h}\]

고등학교 수학시간에 배우는 1차함수 미분식인데, 이것을 수치미분(numerical gradient)이라고 합니다.

1차원의 경우가 아닌, 다 차원의 경우 x 가 vector의 형태로 사용하게 됩니다.

이 수치미분 식을 다차원의 형태로 확장하여 코드로 작성하게 되면 다음과 같습니다.

def eval_numerical_gradient(f, x):
"""
a navie implementation of numerical gradient of f at x
- f should be a function that takes a single argument
- x is the point (numpy array) to evaluate the gradient at
"""

fx = f(x)   # evaluate function value at original point
grad = np.zeros(x.shape)
h = 1e-5

# iterate over all indexes in x
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:

    # evalueate function at x+h
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # increment by h
    fxh = f(x) # evaluate f(x + h)
    x[ix] = old_value # restore to previous value (very important!)

    # compute the partial derivative
    grad[ix] = (fxh - fx) / h # the slope
    it.iternext()   # step to next dimension

return grad

그렇지만 위와같이 수치미분으로 값을 계산하게 되면 정확한 값을 구할 수 없고(i.e. 근사치를 구하게 됨), 또한 loop를 돌면서 값을 하나씩 구하기 때문에 속도가 현저하게 떨어지게 됩니다.

numerical gradient’s feature

  • approximate
  • very slow to evaluate

우리가 구하려고 하는 것은 W의 변화량에 따른 loss 의 변화량이기 떄문에, 결과적으로 위와 같이 수치미분을 하여 값을 구하는 것은 어리석은 방식입니다.

때문에 실제로는 다음과 같이 analytic gradient를 이용하게 됩니다.

\[\begin{aligned} & L = \frac{1}{N}\sum_{i=1}^{N} L_i + \sum_k W_k^2 \\ & L_i = \sum_{j \ne y_i} max(0, s_j - s_{y_i} + 1) \\ & s = f(x; W) = Wx \\ \\ & \nabla wL\\ \end{aligned}\]

Summary

이렇게 수치미분과 해석미분에 대해서 알아보았는데 각 특징을 정리하면 다음과 같습니다.

  • 수치미분(Numerical gradient)은 근사치이고 느리지만 구현이 쉽다.
  • 해석미분(Analytic gradient)은 정확하고 빠르지만 구현이 어렵다(error-prone).

따라서, 실제로는 항상 해석미분을 사용하여 미분 값을 구하고 수치미분을 이용해서 해석미분을 한 결과가 오류가 없는지 확인하는 방식(i.e. gradient check)으로 사용하게 됩니다.

경사하강법(Gradient Descent)

다시 돌아와 경사하강법(Gradient Descent)를 코드로 살펴보게 되면 다음과 같습니다.

# Vanilla Gradient Descent

while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += - step_size * weights_grad   # perform parameter update

위 코드를 한번 살펴보면, step_size 는 learning rate로 수식에서는 일반적으로 $\alpha$ 로 표현이 되는 것이고, gradient 의 값만큼 $W$를 감소시켜 주어야 하기 때문에 - 부호를 붙여서 weight 에서 해당 값을 빼주게 됩니다.

learning rate 와 앞에서 살펴봤던 regularization strength 값은 가장 골치아픈 hyperparameter 값으로, validation set을 이용해서 최적의 값을 찾아주어야 하는 것이 필요합니다.

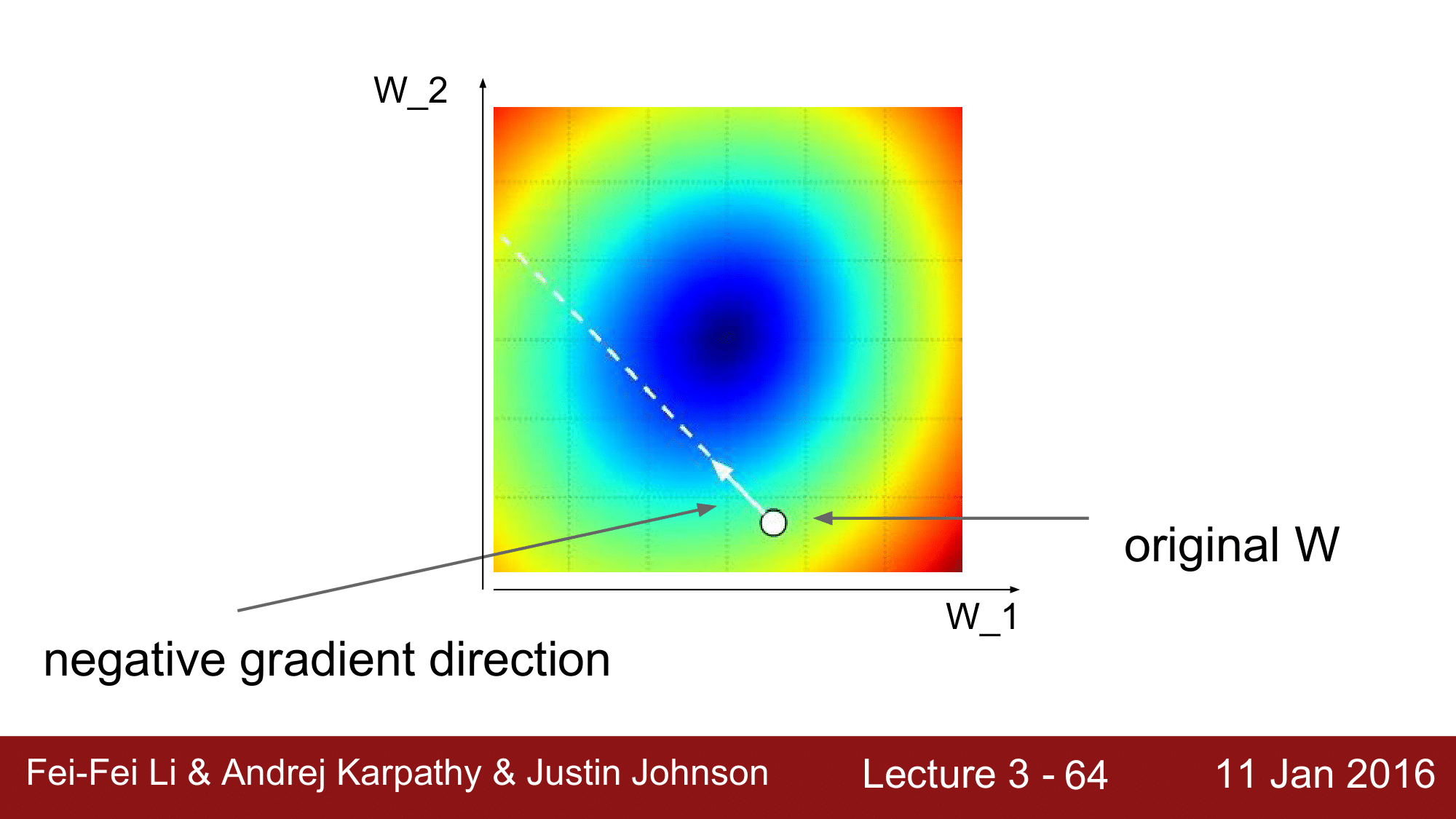
그림을 통해 살펴보면, original W 가 음의 gradient 방향으로 계속 이동을 하면서 $W$를 계속해서 최적화를 해 나가는 것이 gradient descent가 되겠습니다.

미니배치를 이용한 경사하강법(Mini-batch Gradient Descent)

앞에서 설명했던 Gradient Descent는 full-batch gradient descent입니다.

현실에서는 보통 Mini-batch Gradient Descent를 사용하여 $W$를 업데이트 하는데, 한번에 모든 Training Set을 메모리에 올려서 Gradient Descent를 진행하는 것이 비효율적이기 때문입니다. 따라서 미니배치를 이용하여 training set을 여러개의 작은 batch로 나누어 wegiht를 계속해서 수정해나가는 방식으로 기울기 감소를 진행합니다.

코드로 보면 다음과 같습니다.

# Vanilla Minibatch Gradient Descent

while True:
    data_batch = sample_training_data(data, 256)    # sample 256 examples
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += - step_size * weights_grad   # perform parameter update

일반적으로 mini-batch size는 32/64/128과 같은 값으로 진행을 하게 됩니다.

AlexNet(2012)에서는 256개의 mini-batch를 활용했다고 합니다. 여기서 mini-batch size를 어떻게 정할 것인가에 대한 것은 하이퍼파라미터까지는 아니고 학습을 진행하는 하드웨어 환경(cpu, gpu, meomory size)를 고려해서 설정해주면 됩니다.

학습률(Learning rate)

여기서 잠깐 learing rate가 기울기 학습에 미치는 영향에 대해 살펴보겠습니다.

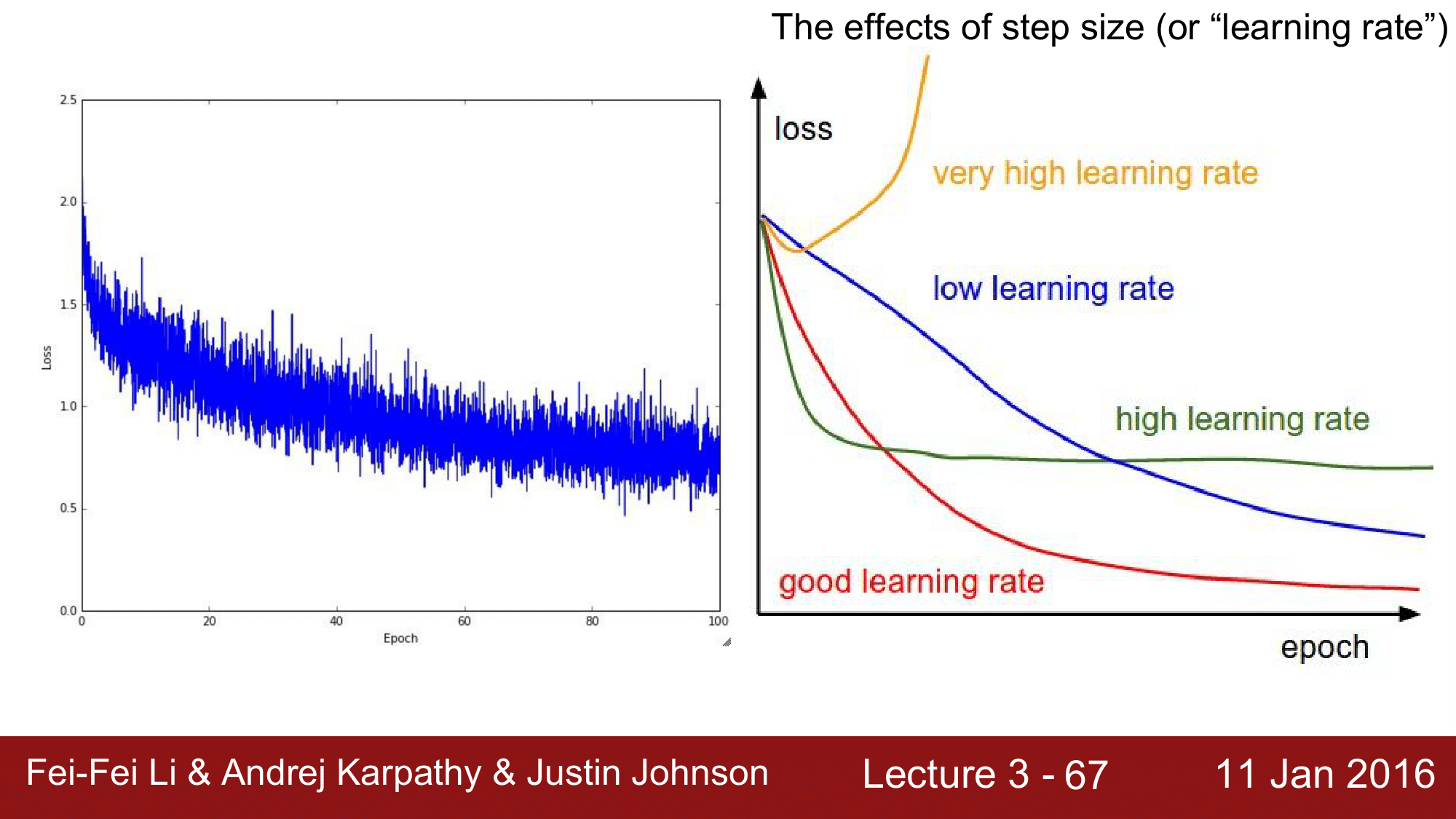
좌측의 그래프는 시간이 증가함에 따라 loss 가 전반적으로 감소하는 것을 보여주는 것인데, 값이 위아래로 왔다갔다 하는 것을 볼 수 있습니다. 이는 미니배치를 사용하므로써 보이는 노이즈 입니다.

이런 노이즈가 생기는 이유는 특정 mini-batch size만큼의 한정적인 데이터만을 가지고 $W$를 업데이트 하기 때문에 경우에 따라 loss 가 잠깐 증가하거나 감소하는 것이 반복되어서 그렇습니다.

하지만 장기적으로 보았을 떄 loss 가 서서히 내려가면서 올바른 값을 찾아가는 것을 볼 수 있습니다.

우측의 그래프는 learing rate 값을 어떻게 설정하느냐에 따라 loss 값이 어떻게 변하게 되는지를 보여주는 그래프입니다.

만약에 lr(learning rate)를 너무 크게 잡게 되면, 보이는 바와 같이 loss 가 감소하는 것이 아니라 diverge 하거나 explode 하는 것을 볼 수 있고, lr을 너무 작게 잡게 되면 loss 가 최저점까지 걸리는 시간이 너무 오래걸린다는 것(slow convergence)을 볼 수 있습니다.

또한 lr이 좀 높은 경우에는 loss가 최저점에 도달하지 못하는 것을 볼 수 있습니다. 이런 경우 global minimum 지점에 빠지지 않고 local minimum 지점에 빠지게 된 경우라고 할 수있습니다.

마지막으로 lr을 적절하게 두게 되면, 빠른 시간 내에 loss 가 최소화되는 것을 확인할 수 있습니다.

위 그래프를 보면 알 수 있듯이 learing rate를 설정하는 것은 매우 어렵기 떄문에 lr 을 높은 값에서 부터 낮은 값으로 decay해 나가며 적절한 lr 값을 설정하는 경우가 많습니다.

이런 Mini-batch Gradient Descent의 대표적인 예로 stochastic GD라는 것이 있고, 파라미터를 업데이트 하는 방법으로 Gradient Descent만 있는 것이 아니라 Momentum, Adagrad, RMSProp, Adam 등이 있습니다.

예를 들어 Momentum 같은 경우, loss 가 줄어드는 속도까지 고려하여 진행하기 때문에 더 빠르게 loss 의 최소치에 도달할 수 있습니다. 이러한 다양한 방법에 대해서는 이후 Lecture.4에서 설명하겠습니다.

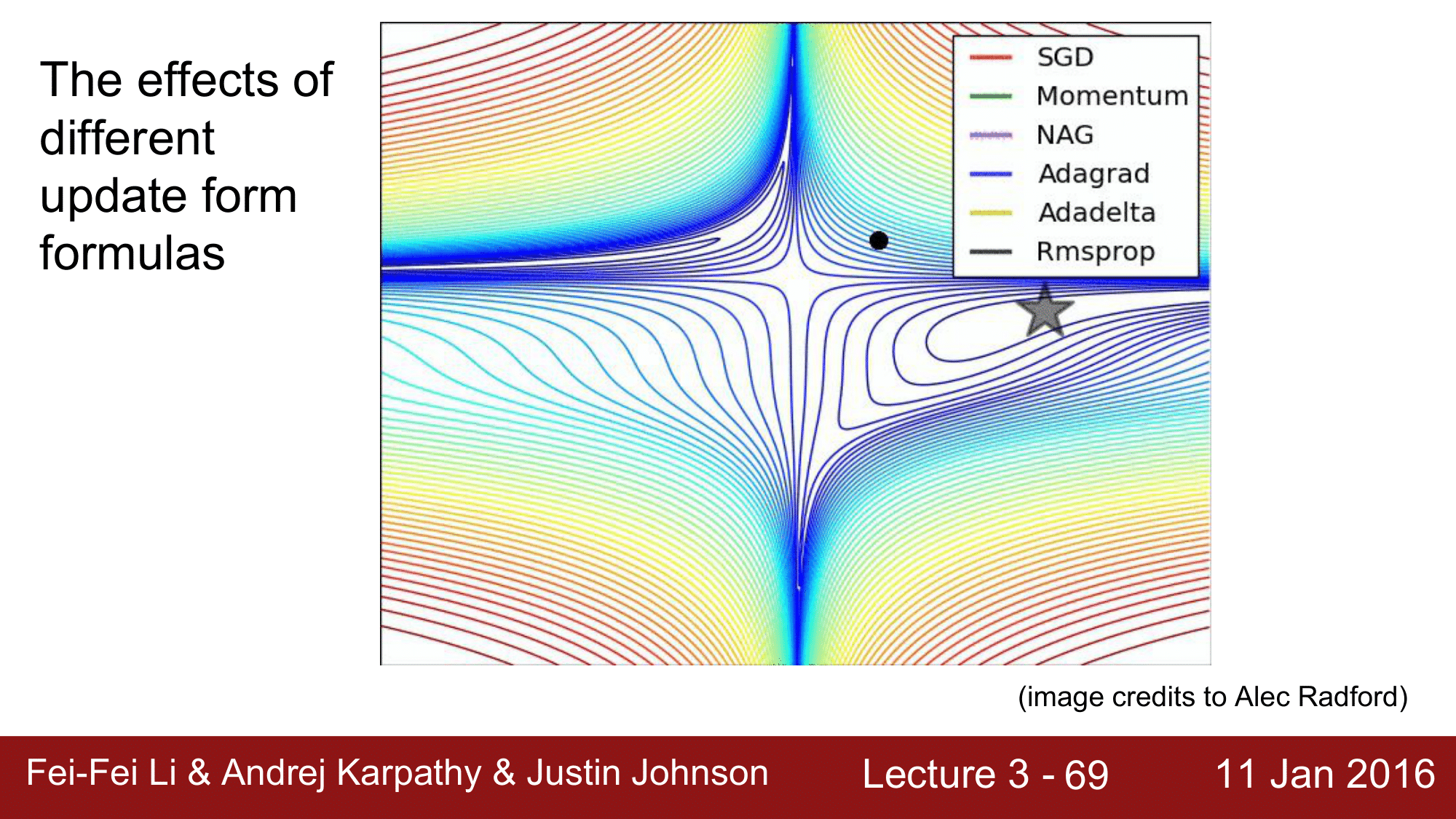
위 이미지는 각 formula들이 어떠한 방식으로 최저치를 찾아가는지를 보여줍니다.

여기서 SGD의 경우 끝없이 계속해서 값을 찾아가는 것을 볼 수 있듯이 굉장히 느리게 진행됩니다. 그리고 Momentum의 경우 아래까지 over-shooting을 했다가 빠르게 목표치까지 도달하는 것을 볼 수 있습니다.

Image Classification 의 고전적 방법

지금부터는 CNN(Convolutional Neural Network)이 나오기 이전에 사용했었던 이미지 분류 방법에 대해 참고로 알아보겠습니다.

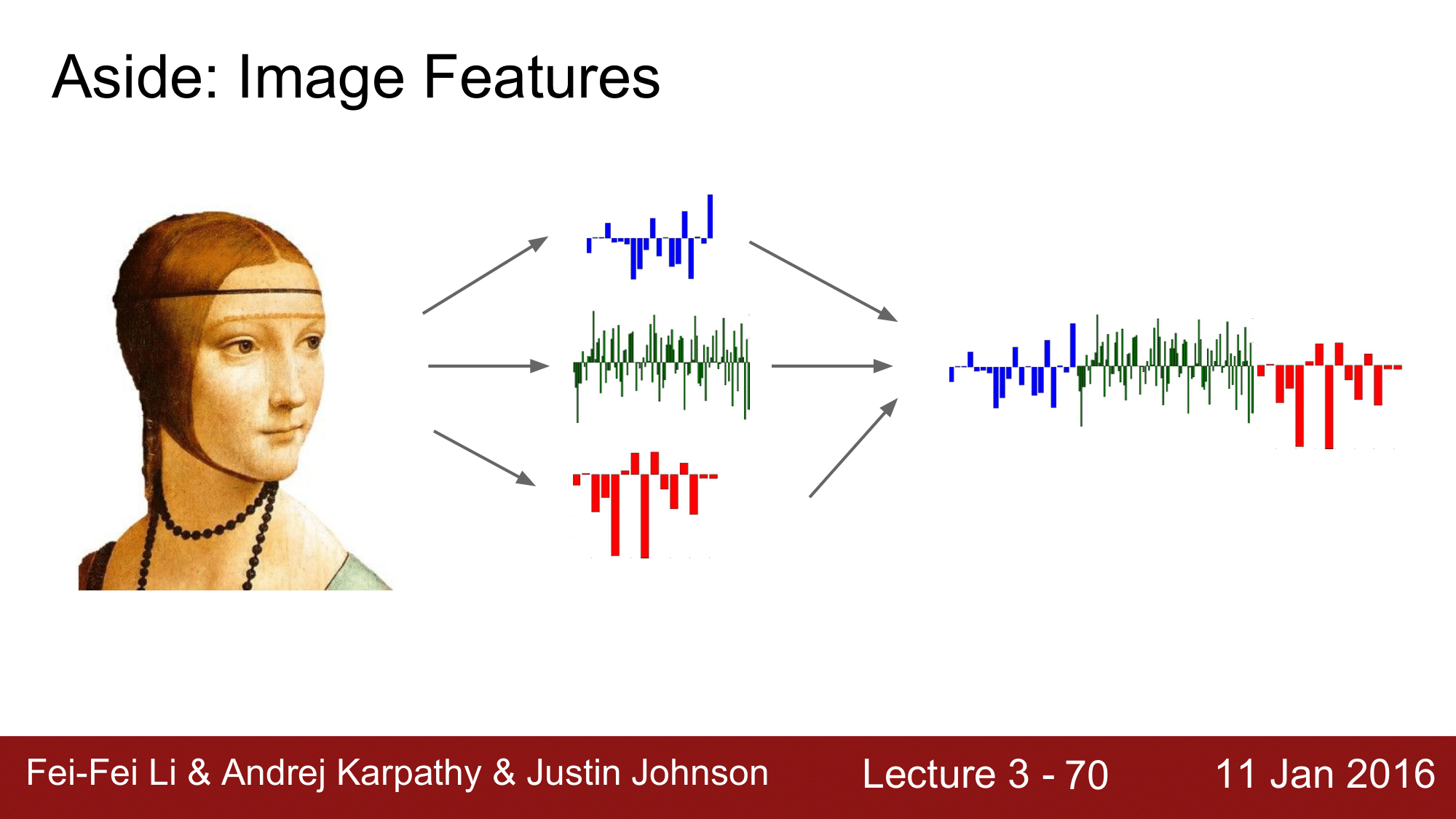
전통적인 방식에서도 CNN에서와 같이 Linear Classifier를 이용했습니다. 하지만 모든 이미지를 커버해야 했기 때문에 Original Image 에 적용하지는 않았고, Image로 부터 feature를 추출하여 거기에 Linear Classifier를 적용했습니다.

먼저 Hog, Color histogram 과 같은 feature를 추출하고 이들을 gient color vector처럼 결합시킵니다. 그 다음 결합된 vector를 Linear Classifier 에 적용을 합니다.

이것이 일반적인 방법이었습니다.

그래서 feature를 추출하는 방식을 보게 되면 다음과 같습니다.

Color (Hue) Histogram

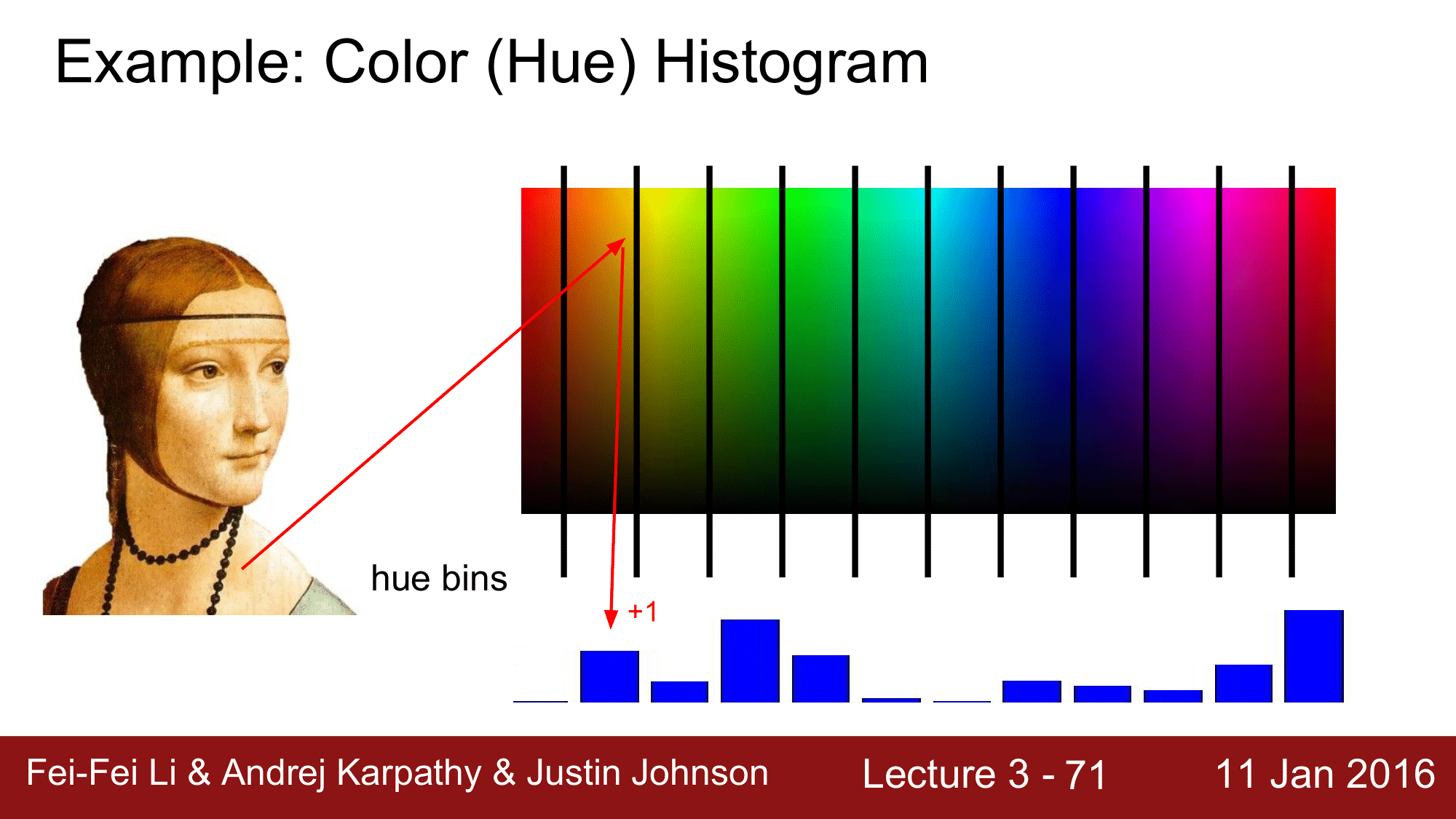
첫번째가 바로 Feature Histogram 인데, 이때 feature 가 color가 됩니다.

위와 같이 이미지가 있을 때, 먼저 모든 pixel 들의 color를 파악을하고, 그 전체 color 파노라마에 대해 각각에 color에 해당하는 bin이 몇 개 인지 count하여 feature를 추출하는 방식입니다.

Hog/SIFT features

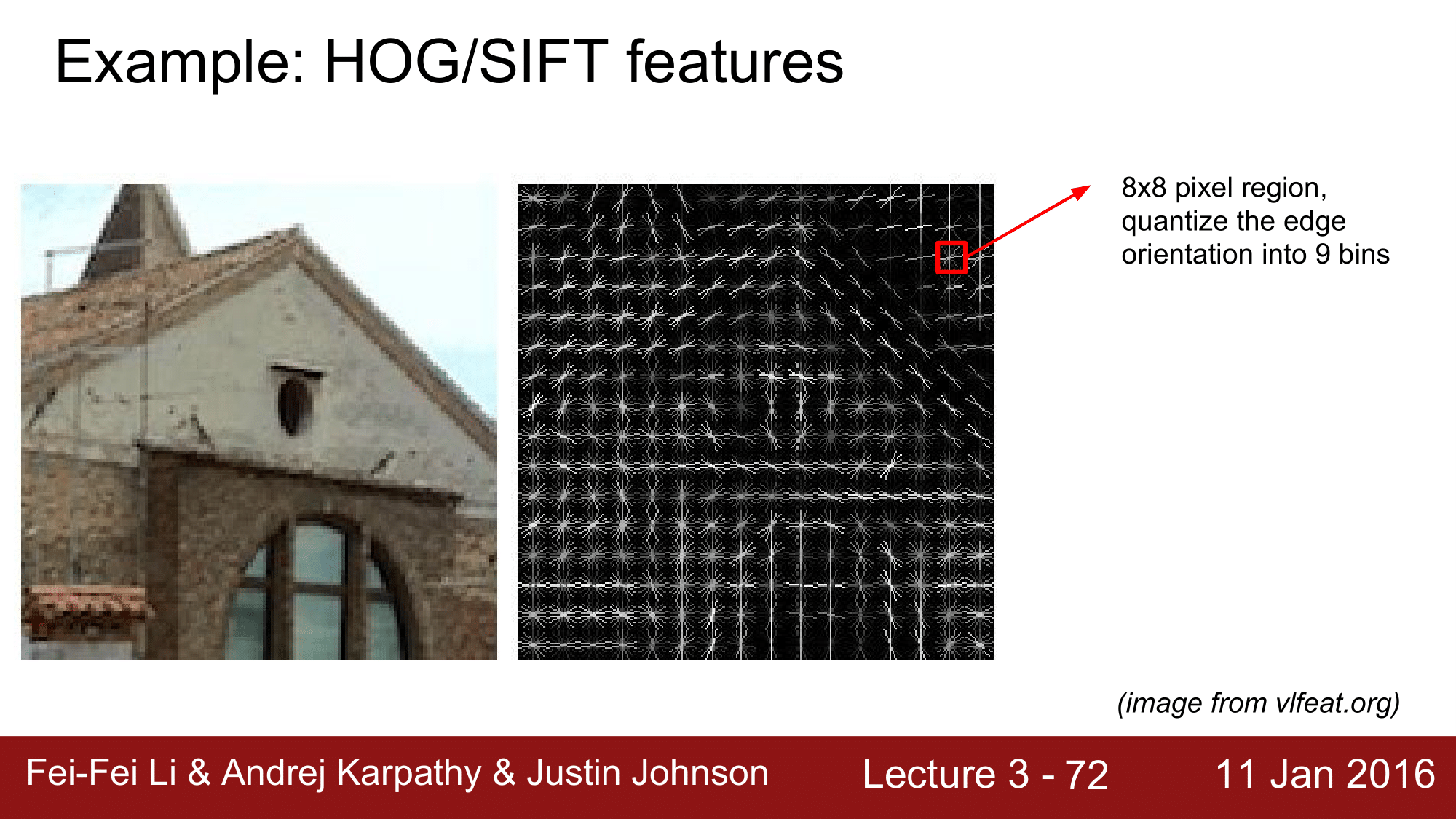
두번째로 Feature를 추출하는 방식은 Hog/SIFT 방식입니다.

이는 주로 엣지(Edge)의 방향; Orientation을 feature로 추출하는 것인데, 오른쪽 그림과 같이 8x8 pixel 로 되어있는 부분을 보면서 엣지들의 방향을 총 9가지로 구분하여, 9가지의 bin에 총 몇개가 속하는가를 기준으로 해서 edge의 orientation을 feature로 추출하는 방식입니다.

이와 유사한 방식으로 GIST, LBP, Texton SSIM 등 과같은 방식이 존재합니다.

Bag of Words

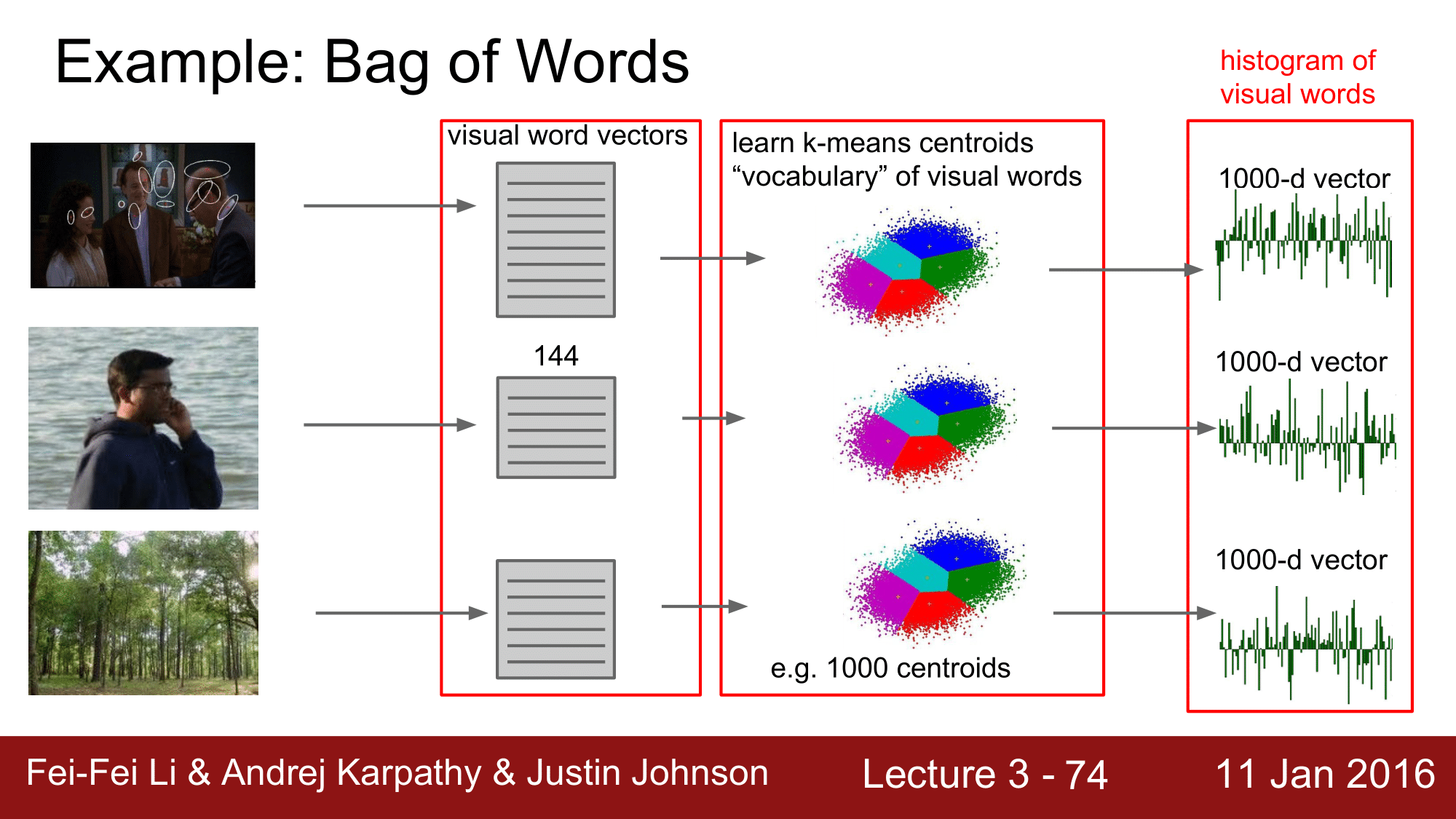
세번째 방법으로는 Bag of Words 라는 방식이 있습니다.

이 방식은 가장 왼쪽의 각 이미지의 지점들을 보고 그 작은 local patch들을 frequency, color와 같은 featrue 에 대해 vector로 기술합니다. 이렇게 기술된 vector를 모아 dictionary 화 합니다. 이렇게해서 생성된 dictionary 들 중 테스트하려는 이미지와 가장 feature 가 유사한 vector를 k-means를 이용하여 dictionary 내에서 찾습니다. 그렇게 하여 feature들을 추출하고 concatenation을 한 다음 Linear Classifier를 적용해주는 방식입니다.

Summary

이처럼 전통적인 방식에서는 여러가지 방식을 이용하여 Feature를 Extraction하고 이것들을 concatenation 해준 다음에 Linear Classifier의 인자로 던져줌으로써 결과값을 얻습니다.

하지만 우리가 접근하고 있는 Deep Learning 방식에서는 위 전통적인 방식들과는 다르게 Feature 추출을 임의의 방식으로 하는 것이 아니라 Original Image를 Classifier에 넣어 Training 된 Model이 결과값을 알아서 출력해주는 방식인 것입니다.

다음시간에는 역전파(Backpropagation)와 신경망(Neural Network)에 대해 알아보겠습니다.

Twitter, Facebook