해당 포스트는 송교석 님의 유튜브 강의를 정리한 내용입니다. 강의 영상은 여기에서 보실 수 있습니다.
Image Classification

Image Classification 이란 이미지를 보고 어떠한 이미지인지 분류하는 것을 의미합니다.
이를 이용하여 detection과 segmentation 을 진행하게 됩니다.
이미지 분류를 위해서는 이미지가 어떻게 구성되는 지 알아야 합니다.
이미지는 0부터 255사이의 값을 갖는 숫자로 구성된 3차원 array 로 표현됩니다. (width, height, color-channel)로 표현되는데 이떄, color-channel 은 RGB 색상값을 의미합니다.
이렇게 구성된 이미지에서 해당 이미지가 어떠한 이미지인지 분류하는 과정에서 다음과 같은 도전과제들이 존재합니다.
- lilumintaion: 조명의 차이
- Deformation: 형태의 변형
- Occlusion: 은폐, 은닉
- Background clutter: 배경과 구분이 안되는
- Intraclass varitation: 동종 내에서의 판별
def prediction(image):
# some code...
return class_label
이미지 분류에서는 위와 같은 어려움이 있기 떄문에, 고양이나 다른 class들을 인지하기 위한 알고리즘을 하드코딩해서 사용한다는 것은 매우 어렵습니다.

물론 하드코딩으로 물체를 검출하려고 했던 사례가 있었습니다. 이미지 내의 엣지를 검출해서 해당 엣지의 배열 특징을 이용해, 전반적인 이런 상태를 다른 이미지 데이터와 비교해서 분석하려고 했으나 스케일업이 불가능한 확연한 단점이 존재했습니다.
이후 데이터기반 접근방법(Data-driven approach)을 통해 이미지를 분류하기 시작했습니다.
해당 방법은 다음과 같습니다.
- 이미지와 레이블을 데이터셋으로 준비함
- 이미지 분류기를 머신러닝을 이용해서 훈련시킴
- 테스트 이미지를 이용해 해당 분류기를 평가함
하드코딩으로 이미지로 부터 곧 바로 물체를 검출하려고 했던 방법과는 다르게, 이 방법에서는 학습과 예측의 두 단계로 분리하여 물체를 검출하게 됩니다.
def train(train_images, train_labels):
# build a model for images -> labels ...
return model
def predict(model, test_images):
# predict test_lables using the model ...
return test_labels
데이터 기반 접근 방법
1. Nearest Neighbor Classifier
데이터 기반 접근 방법의 첫번째로 Nearest Neighbor Classification을 살펴보겠습니다.
이 방법은, 모든 학습용 이미지와 레이블들을 메모리에 올리고, 테스트 이미지를 모든 트레이닝 이미지와 비교해서 가장 비슷한 이미지의 레이블과 같다고 예측을 내리는 방법입니다.

위의 슬라이드는 CIFAR-10의 데이터 셋을 이용하여 트레이닝하고 테스트한 결과를 보여줍니다.
해당 데이터 셋은 10개의 label, 32x32 size의 이미지로 구성되어 있으며, 50000개 training set과 10,000개 test set으로 나뉘어져 있습니다.
좌측의 테스트이미지를 기준으로 트레이닝 이미지 중 가장 비슷한 10개의 이미지를 추출하여 예측하는 방식입니다.
테스트 이미지를 모든 트레이닝 이미지와 비교한다고 했는데, 이를 위해 L1 distance를 사용합니다.
- L1 distance 는 manhattan distance 라고도 불리우는데, 동작방식은 다음과 같습니다.
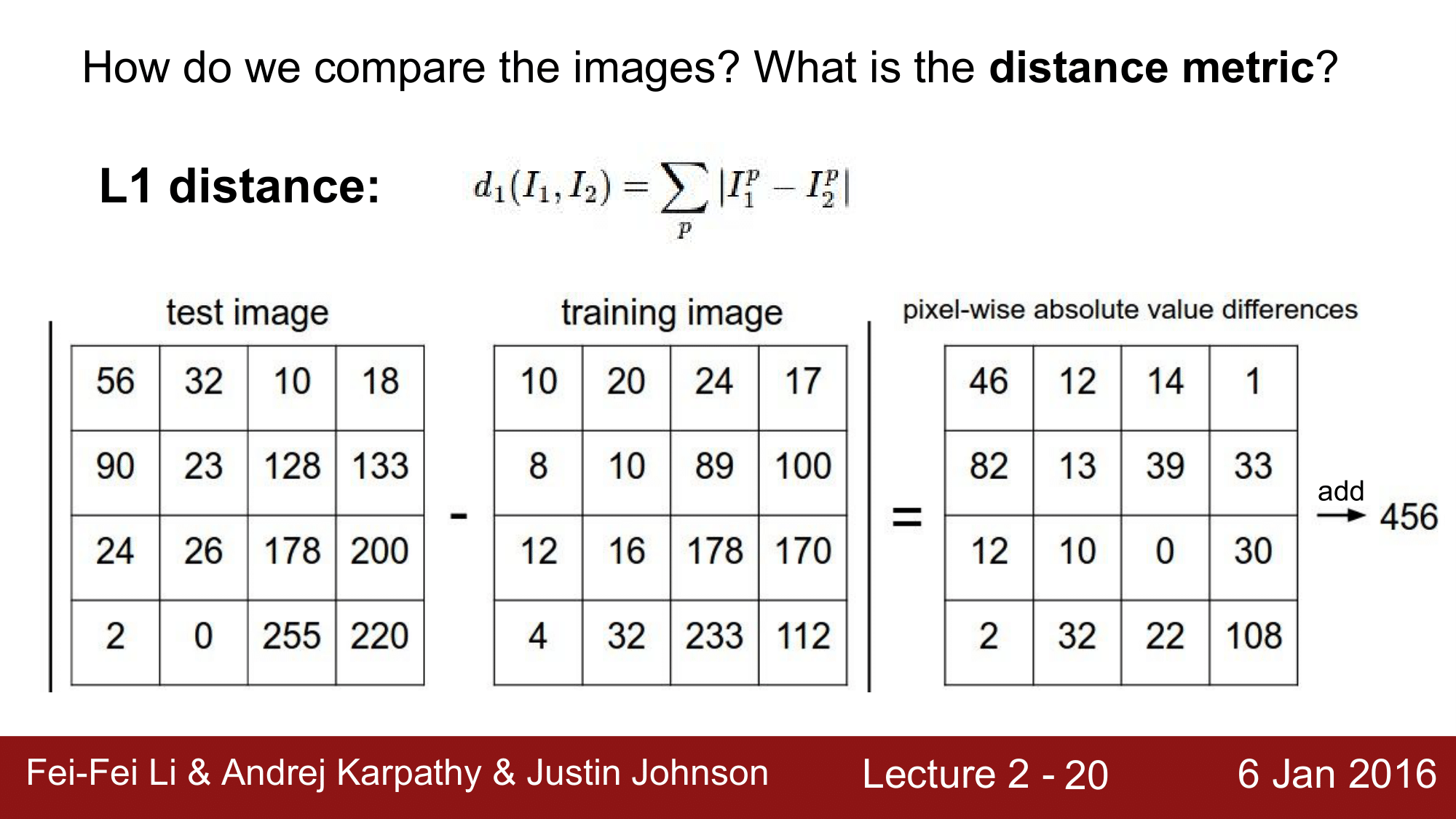
테스트 이미지와 트레이닝 이미지 각각의 원소들간의 차에 대한 절대값을 먼저 구하고, 해당 결과에서의 원소들을 모두 더하는 방식으로 L1 distance를 구하게 됩니다.
이를 이용하여 Nearest Neighbor classifier 를 python code로 다음과 같이 구현할 수 있습니다.
import numpy as np
class NearestNeighbor:
def __init__(self):
pass
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
self.Xtr = X
self.Ytr = Y
def predict(self, X):
""" X is N x D where each row is an example we wish to predict label for """
num_test = X.shape[0]
# lets make sure that the output type matches the input type
Ypred = np.zeros(num_test, dtype=self.ytr.dtype)
# loop over all test rows
for i in xrange(num_test):
# find the nearest training image to the i'th test image
# uisng the L1 distance (sum of absolute value differences)
distances = np.sum(np.abs(self.Xtr - x[i, :]), axis=1)
min_index = np.argmin(distances) # get the index with smallest distance
Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
return Ypred
학습단계에서는 모든 트레이닝 데이터를 메모리에 올려 해당 데이터를 기억해둡니다.
- X: 이미지
- Y: 해당 이미지의 레이블
예측단계에서는
- X: 테스트 이미지 distances 는 테스트 이미지 한장을 모든 트레이닝 이미지와 비교를 해서 L1 distance 를 계산합니다.(numpy의 broadcasting 을 이용)
이후 L1 distacne가 가장 작은 트레이닝 이미지를 찾아서 테스트 이미지를 예측합니다.
하지만 이 방법을 이용하게 되면 물체 검출에서 큰 문제가 발생하는데, 그 이유는 다음과 같습니다.
위 처럼 트레이닝 데이터를 메모리 상에 올려서 각각에 대해 테스트 데이터와 비교하는 방식을 사용하게 되면 트레이닝 데이터 사이즈에 따라 분류 작업의 속도는 Linear 하게 변하게 되는데 Object Detection 에서는 트레이닝 속도보가 테스트 속도가 더 중요하기 때문에 이 방법은 거의 사용되지 않습니다.
이후 소개할 CNN의 경우는 위의 경우와는 반대로 트레이닝 테이터셋의 크기와는 무관하게 예측단계에서는 O(1) time 이 걸립니다.
앞서 소개한 L1 distance 와는 다르게 L2 distance라는 것도 존재하는데, L1 distance 와 L2 distance의 수식을 비교해보면 다음과 같습니다.
- L1 (Manhattan) distacne
- L2 (Euclidean) distance
주어진 환경에서 여러번의 실험을 통해 최적의 파라미터를 찾아야 한다는 점에서 위 두 distance 모두 하이퍼파라미터라고 할 수 있습니다.
2. KNN(k-Nearest Neighbor)
앞서 살펴 본 Nearest Neighbor 에서는 테스트 이미지와 가장 거리가 짧은 트레이닝 이미지를 고르는 방식으로 테스트 이미지가 어떤 종류의 이미지인지 판별하였습니다. 이런 방식과는 다르게 KNN 은 k 개의 가장 가까운 이미지들을 찾고 이 k개의 이미지들이 다수결로 vote를 하여, 이때 가장 vote 가 많은 것으로 predict 합니다.
그렇다면 KNN 과 Nearest Neighbor 둘 중 어떤 것이 성능이 더 좋은지에 대해 궁금할 수 있는데, 일반적으로 Nearest Neighbor 보다 KNN 이 성능이 더 좋다고 알려져 있습니다.

위 그림을 보면 가운데는 그냥 Nearest Neighbor이고 오른쪽 은 k=5 인 Nearest Neighbor 로 가운데 이미지에 비해 오른쪽 이미지가 좀 더 부드럽게 분류를 수행한것을 알 수 있습니다.

앞서 소개했던 CIFAR-10 의 경우 k=10인 Nearest Neighbor라고 볼 수 있습니다.

일반적으로 테스트셋의 이미지를 Nearest Neighbor의 분류기를 통해 판별하는데, 트레이닝 셋의 이미지로 판별하면 비교하는 대상에 검출하려는 이미지가 그대로 들어가 있기 때문에 정확도는 100%가 됩니다.
그렇다면 Nearest Neighbor 대신에 KNN을 사용하면 어떻게 될까?
답은 Not necessary이다. 즉, 상황에 따라 다르다는 것입이다.
KNN으로 예측을 할때 rank1 은 정확한 값을 예측할 수 있지만, 이후의 rank 가 다른 값을 예측한다면 다수결로 인해 결과적으로는 예측이 바뀔 수 있기 때문에 그렇습니다.
이 외에도 다음과 같은 의문을 가질 수 있습니다.
-
L1 과 L2 distance 중 어떤 것을 선택해야 하는가?
-
KNN의 경우 k를 어떤 값으로 해야 하는가?
즉 하이퍼파라미터를 어떤 값을 설정해야하는가에 대한 의문이 생기게 될 텐데, 이는 문제에 따라 다릅니다. 때문에 각 문제에 대해서 어떤 파라미터가 가장 적절한지 테스트 해보고 선택해야 합니다.

그렇다면 train data, test data 가 있을 때 하이퍼파라미터를 계속 바꿔가면서 test set의 data에 적용을 하면 될까?
이는 매우 위험한 생각인데, 테스트 셋은 마치 최후의 보루처럼 성능평가를 위해 남겨두어야 하기 때문입니다. 이 때문에 hyperparameter를 tuning 하기 위해 validation data 를 train data에서 추출하여 사용합니다(약 20%)
때로는, train data set이 적을 경우 validation data를 따로 두기 어려워지는데 이런 상황에서는 Cross-validation을 이용하여 tuning 하면 됩니다.
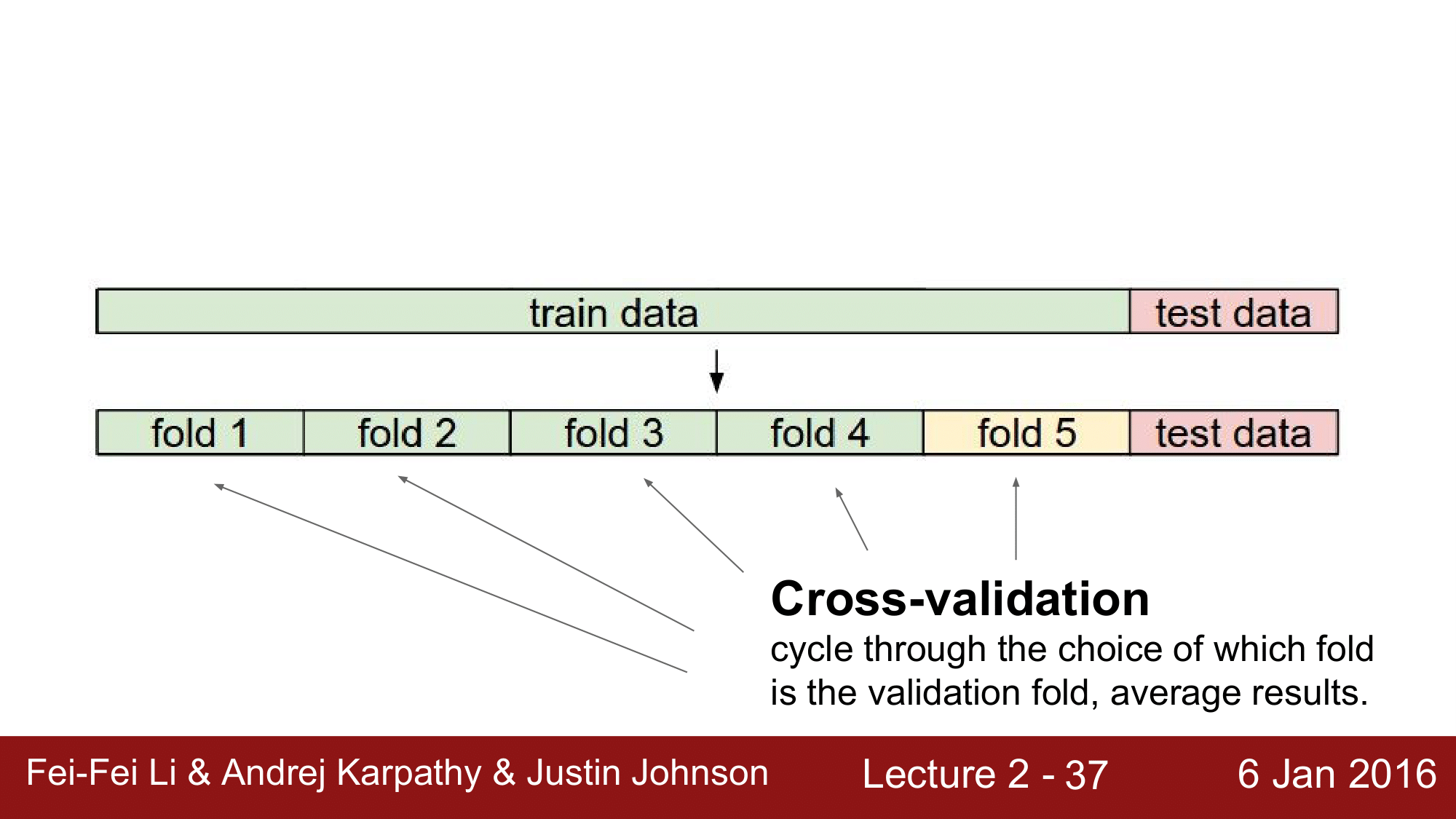
Cross-validation이란, 위와 같이 train data set 을 여러개의 fold로 나눠 각 hyperparamter tuning 과정에서 validation data 를 계속 다른 fold로 선택하여 tuning 하는 방법입니다.
다음 그림은 k에 대해 Cross-validation 결과에 대한 그래프입니다.
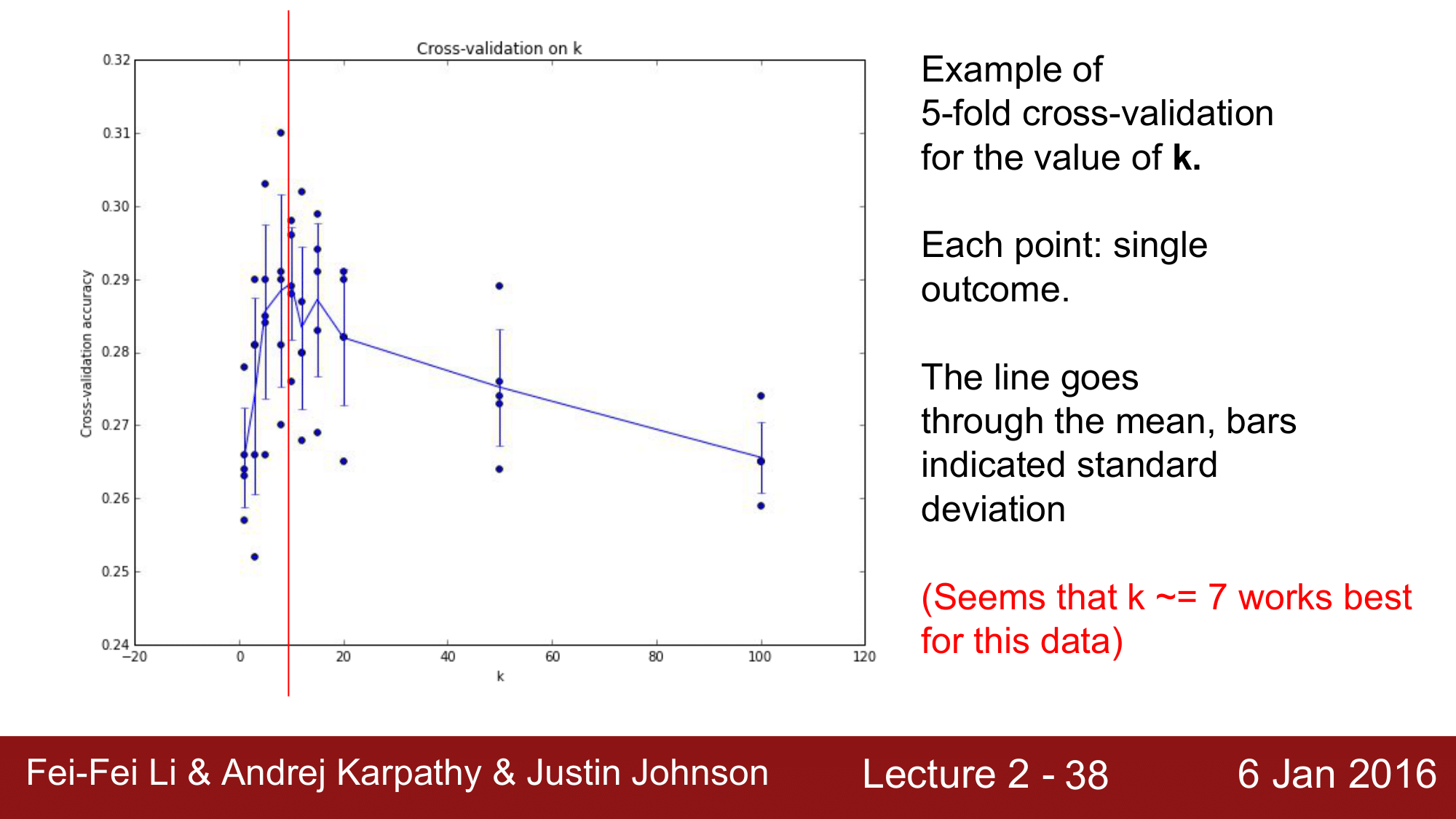
이를 보게 되면 각 k에 대해 5개의 점이 찍혀있는 것을 볼 수 있는데, 해당 점들은 각 테스트에 대한 결과를 나타냅니다. 이 5개 결과에 대한 평균 값을 구해 선으로 연결한 그래프를 보먄 대략 k=7인 점 부근에서 가장 정확도가 높은 것을 볼 수 있습니다. 따라서 k=7로 하여 hyperparameter를 설정해주면 됩니다.
Nearest Neighbor를 처음 소개할 떄 언급했듯이, Nearest Neighbor는 현업에서는 절대 사용하지 않는데, 이유는 다음과 같습니다.
- test time에 대한 성능에 매우 좋지 않다.
- Distance 라는 것이 현실적으로 정확한 예측을 하기 힘들기 때문이다.

위 그림들은 원본이미지와, 그 이미지에 대한 변형인데 2,3,4 번째 이미지가 모두 원본이미지와 같은 L2 distance 값을 갖습니다.
이렇게 원본이미지와 다른 이미지가 같은 distance 값을 갖기 때문에 현실에서는 k-Nearest Neighbor를 사용하지 않는 것이죠.
Linear Classification
Linear Classification은 이후 가장 중요하게 다룰 CNN으로 가는 시작점입니다.

Image Captioning 은 CNN 과 RNN 이 결합되어서 마치 하나의 네트워크 처럼 동작합니다. CNN 으로 image 로 부터 객체를 탐지하여 주요 단어를 추출하고, 그 단어들을 이용해 RNN 으로 문장을 생성하는 방식으로 이루어집니다.
Parametric approach
우리가 지금까지 살펴봤던 Nearest Neighbor같은 것들은 non-parametetric approach 였지만, 지금부터 하려고 하는 Linear Classification 의 경우 Parameter 기반의 접근 방식을 취하고 있습니다.

위 그림에서 처럼 테스트 이미지가 [32x32x3]로 들어오고 10개의 label로 분류하려고 한다면, Linear classification에서는 다음과 같은 식으로 나타낼 수 있는데 이때 $x$ 는 입력값 즉 검출하려는 이미지가 되고, $W$ 는 parameter가 됩니다.
x가 3072x1 의 형상이고 결과가 10x1 의 형상이므로 W는 10x3072의 형상으로 나타내야 함을 알 수 있습니다.
예를 들어 이미지가 4pixel이고 3개의 클래스로 분류한다고 하면 다음 그림과 같습니다.
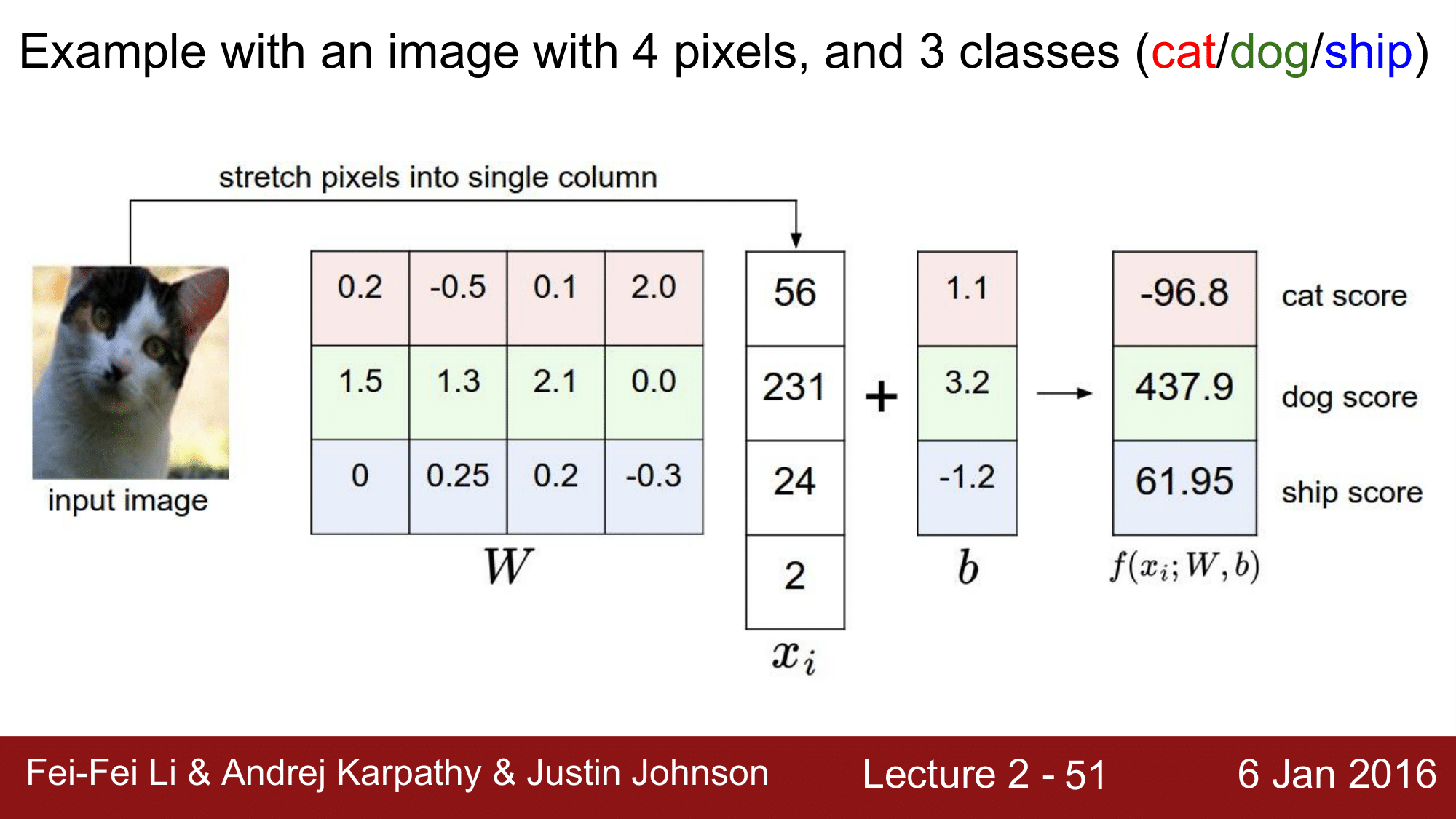
$x$ 가 $(4, 1)$ 이고 $f(x_i, W, b)$ 가 $(3,1)$ 이므로 $W$ 의 형상을 $(3, 4)$ 로 맞춰줍니다. 이후 행렬 연산을 하게 되면 $f$ 의 결과로 각 클래스에 대한 score를 얻게 되는데 고양이 이미지가 입력으로 들어갔음에도 고양이 값이 가장 낮게 나온 것을 알 수 있습니다. 따라서 위의 결과에서는 학습이 제대로 이루어 지지 않았다고 판단할 수 있게 됩니다.
여기서 Linear Classifier 의 성능을 한번 짚고 넘어가 보겠습니다.
Linear Classifier를 말로 풀어서 표현하면 “Just a weighted sum of all the pixel values in the image”라 할 수 있습니다. 다른 말로 “각각 다른 공간적 위치에 있는 color를 couting한 것”라고 할 수 있죠. 이처럼 Linear Classifier에서 color는 대단히 중요한 의미를 갖습니다.
다음은 CIFAR-10의 데이터를 선형회귀를 이용하여 학습된 weights를 시각적으로 표현한 것인데, car의 경우 빨간색 차가 학습데이터로 많이 있었고 horse 의 경우 왼쪽을 보고 있는 데이터가 많이 학습되었음을 알 수 있습니다.

만약, 위 처럼 학습된 weights를 가지고 노란색 차를 test 데이터로 classification을 진행하게 된다면 car로 분류되는 것이 아니라 frog로 분류 될 가능성이 높을 것 입니다.
이 처럼 Linear Classification을 단독으로 사용하게 되면 분명한 한계가 있음을 알 수 있습니다.

우리가 Linear Classifier 를 해석하는 또 다른 방식은 공간이 있고 그 공간을 각각의 Label로 분할해 주고 있다고 볼 수 있습니다.
이렇게 분할하게 됐을 때 Linear Classifier 로 분할하기 어려운 경우는 초반에 설명했었던 이미지 분류의 Challenge들 처럼 다음과 같습니다.
- Negative Colored Image
- Gray Scaled Image
- Same texture but different color
반대로 Shifted Image 의 경우 쉽게 검출 할 수 있을 것입니다.

위의 이미지를 보게 되면 각 분류에 대한 Score를 볼 수 있는데, 고양이와 개구리의 경우 점수가 잘 나오지 않았고, 자동차의 경우 점수가 잘 나온 것을 알 수 있습니다.
이 점수를 통해 다음에 하게 될 Loss function 을 이용하여 weight를 조절하여 더 정확한 예측을 할 수 있도록 할 것입니다.
다음 포스트에서는 Loss function Optimization ConvNets 를 알아보도록 하겠습니다.
