해당 포스트는 송교석 님의 유튜브 강의를 정리한 내용입니다. 강의 영상은 여기에서 보실 수 있습니다.
이번 포스트에서는 Recurent Neural Network(RNN)에 대해서 알아보도록 하겠습니다.

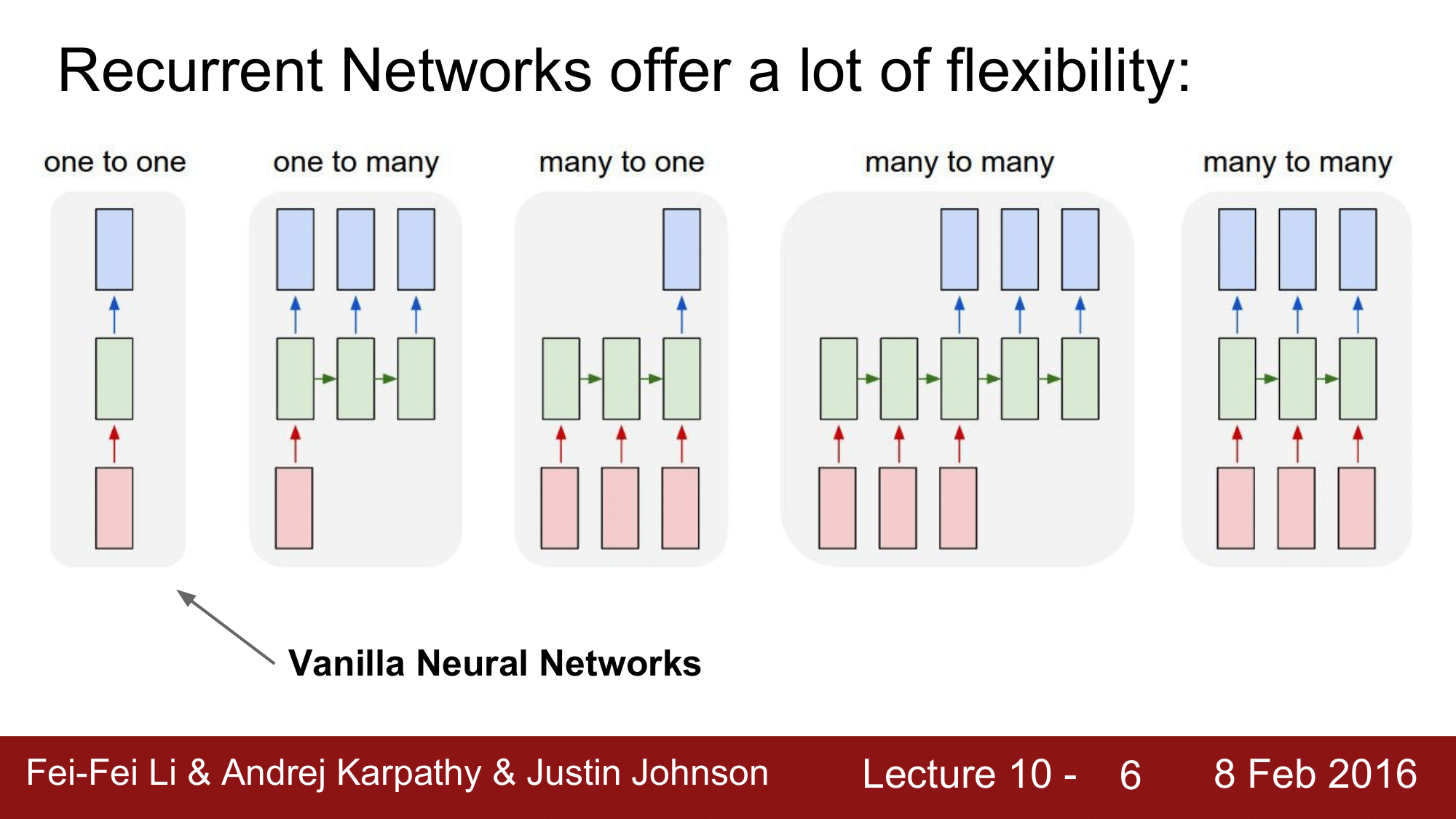
일반적인 Neural Network 은 one to one 의 형태로 input layer, hidden layer, output layer 로 구성이 됩니다. input 레이어에는 일반적으로 fix 된 사이즈의 vector 이미지가 들어가고 hidden 레이어를 거쳐서 output 레이어로 나오게 되는데 output 레이어에서는 input 레이어에서와 마찬가지로 fix 된 사이즈를 갖는 output vector 를 도출해냅니다. 여기 output vector 는 class 의 score 가 됩니다.
그런데, RNN 에서는 이와는 조금 다른 형태로 input 이나 output 에 sequence 를 갖습니다. 위의 그림과 같이 one to many, many to one, many to many 의 형태를 갖는데 각각에 대해 알아보겠습니다.
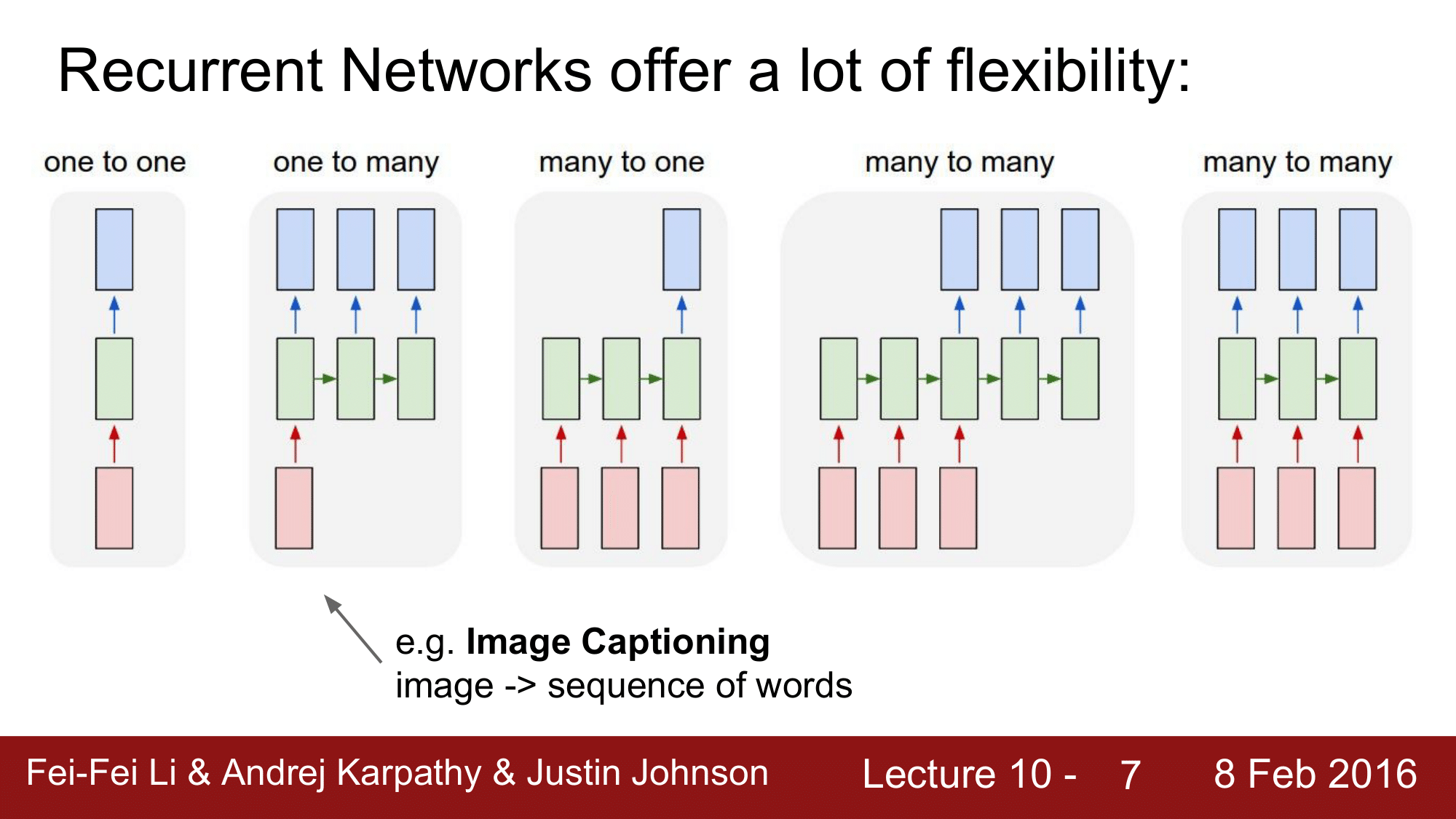
one to many 의 예시로는 Image Captioning 이 있습니다. 즉, 이 이미지를 설명하는 단어들의 sequence 를 출력해냅니다.
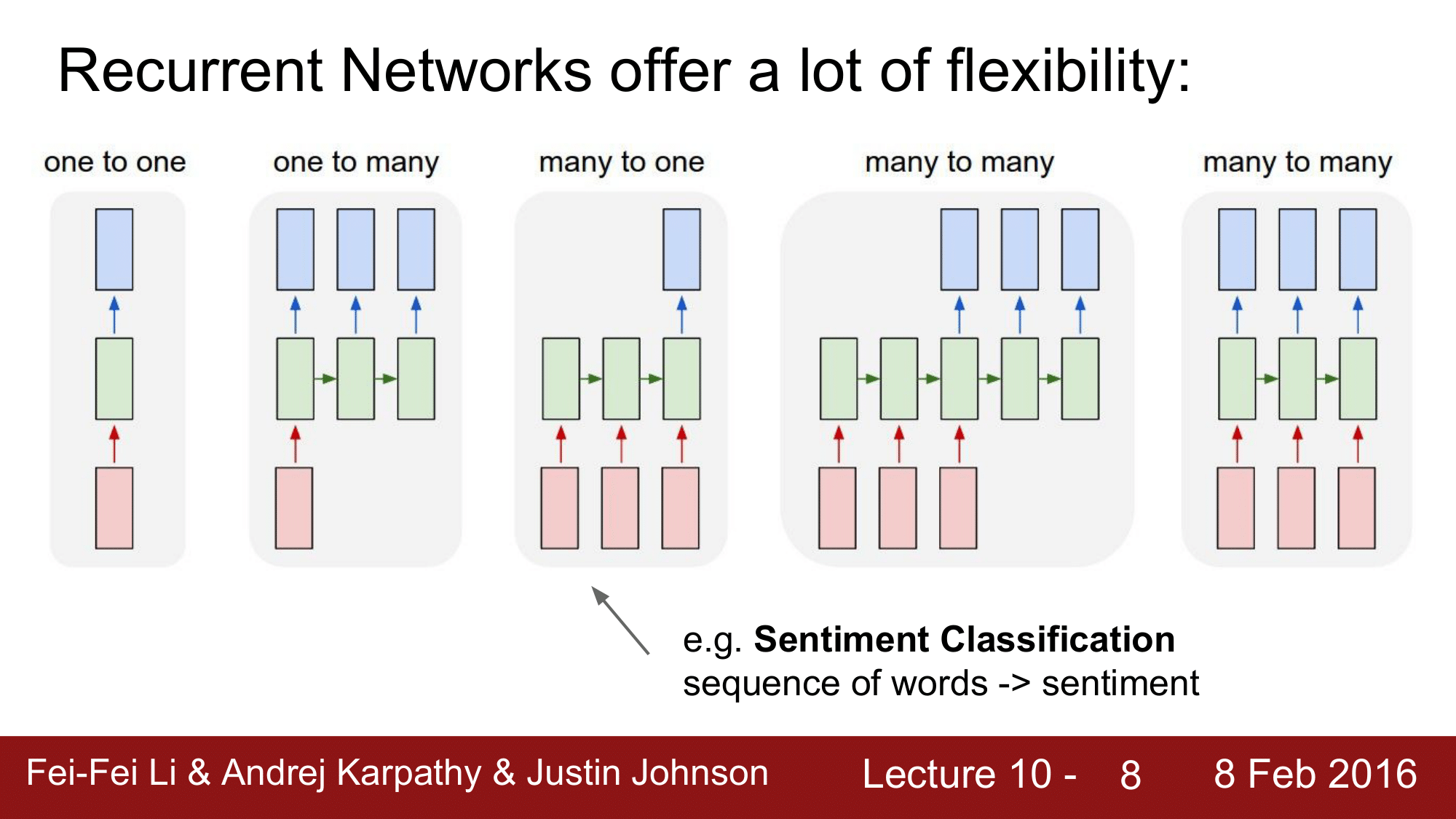
many to one 의 예로는 Sentiment Classification 이 있습니다. 즉, 감정을 분류해내는 것으로 단어들로 구성된 sequence 가 있다고 할 때, 해당 sequence 의 감정이 positive 한지 negative 한지를 하나의 클래스로 분류하는 것이 되겠습니다.
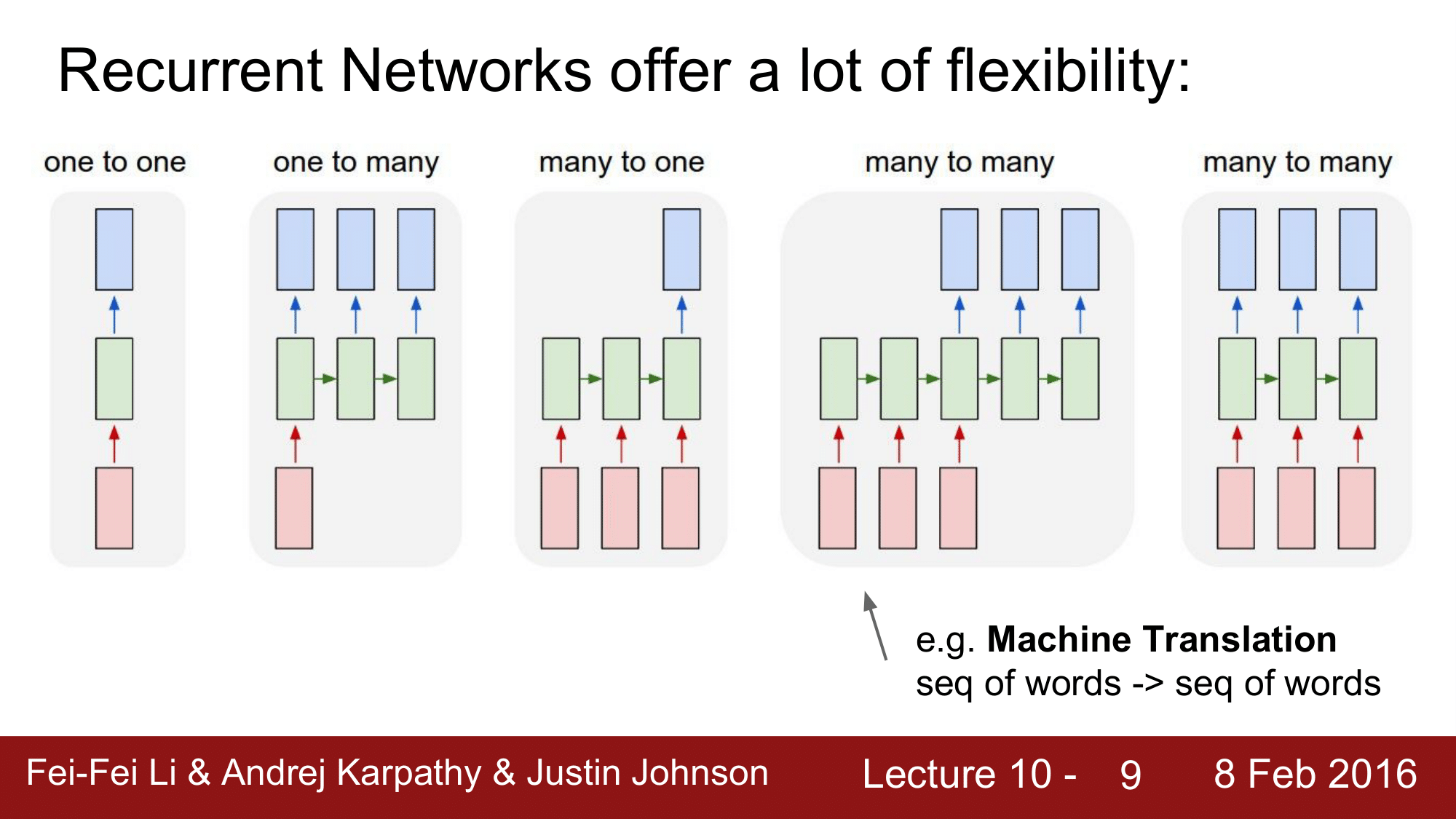
다음으로 many to many 의 예시로는 Machine Translation 이 되겠습니다. 예를 들어, 영어 단어로 구성된 문장이 들어왔을 때, 한국어 단어로 구성된 문장으로 결과를 내놓게 되는 것입니다.
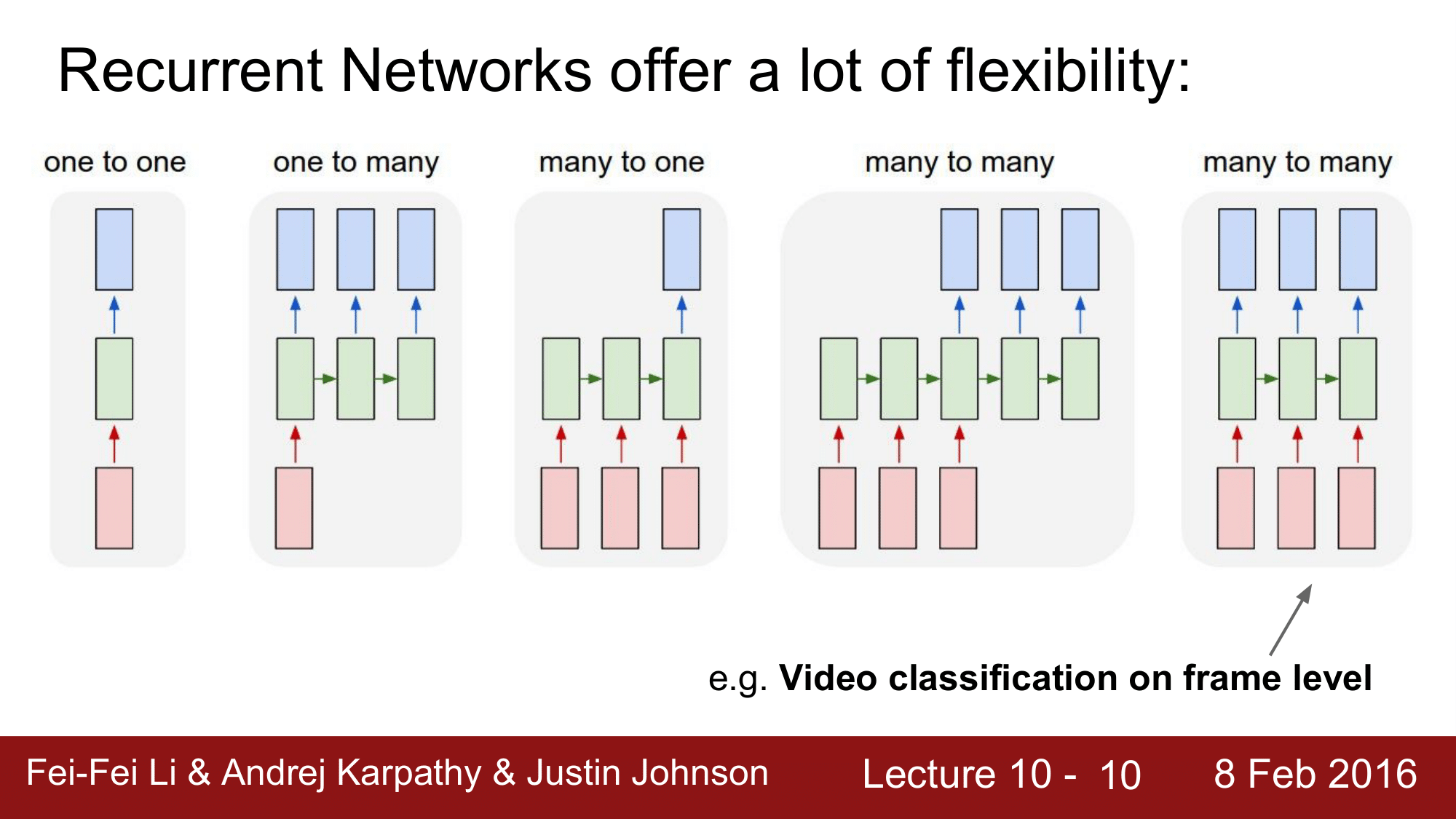
또 다른 many to many 의 예시로는 Video Classification 이 있습니다. 비디오가 input 으로 들어오게 되면 frame level 에서 classify 하게 되는데, 여기서 중요한 것은 예측이 현재 시점에 국한된 함수면 안된다는 것입니다. 비디오에 있어서 예측이라는 것은 현재의 프레임과 prev, next 프레임을 포함한 모든 프레임에 대한 함수가 되어야 한다는 것입니다. 그래서 이처럼, RNN Architecture 의 핵심은 모든 각각의 timestep 에서의 현재의 frame + 지나간 frame 들에 대한 함수로 이루어지게 된다는 것입니다.
한 가지 더 짚고 넘어가자면, one to one 의 일반적인 neural network 의 경우 input 과 output 이 기본적인 sequence 의 형태는 아니지만, IO 의 fixed vector 를 하나의 sequence 로 간주할 수도 있다는 것입니다. 바로 이 예시가 뒤에 나옵니다.

위의 예시는 fixed input 을 sequential 하게 처리한 경우로 Deep Mind 에서 ZIP code 를 인식하기 위해서 만든 모델입니다. 보시면 Convolutional Neural Network 에 큰 이미지를 feed 해서 번지수를 classify 하는 방식으로 하는 것이 아니라, RNN policy 를 이용했습니다. 작은 CNN 을 이용해서 이미지 전체를 sequential 하게 훑어나가는 식으로 진행됩니다.
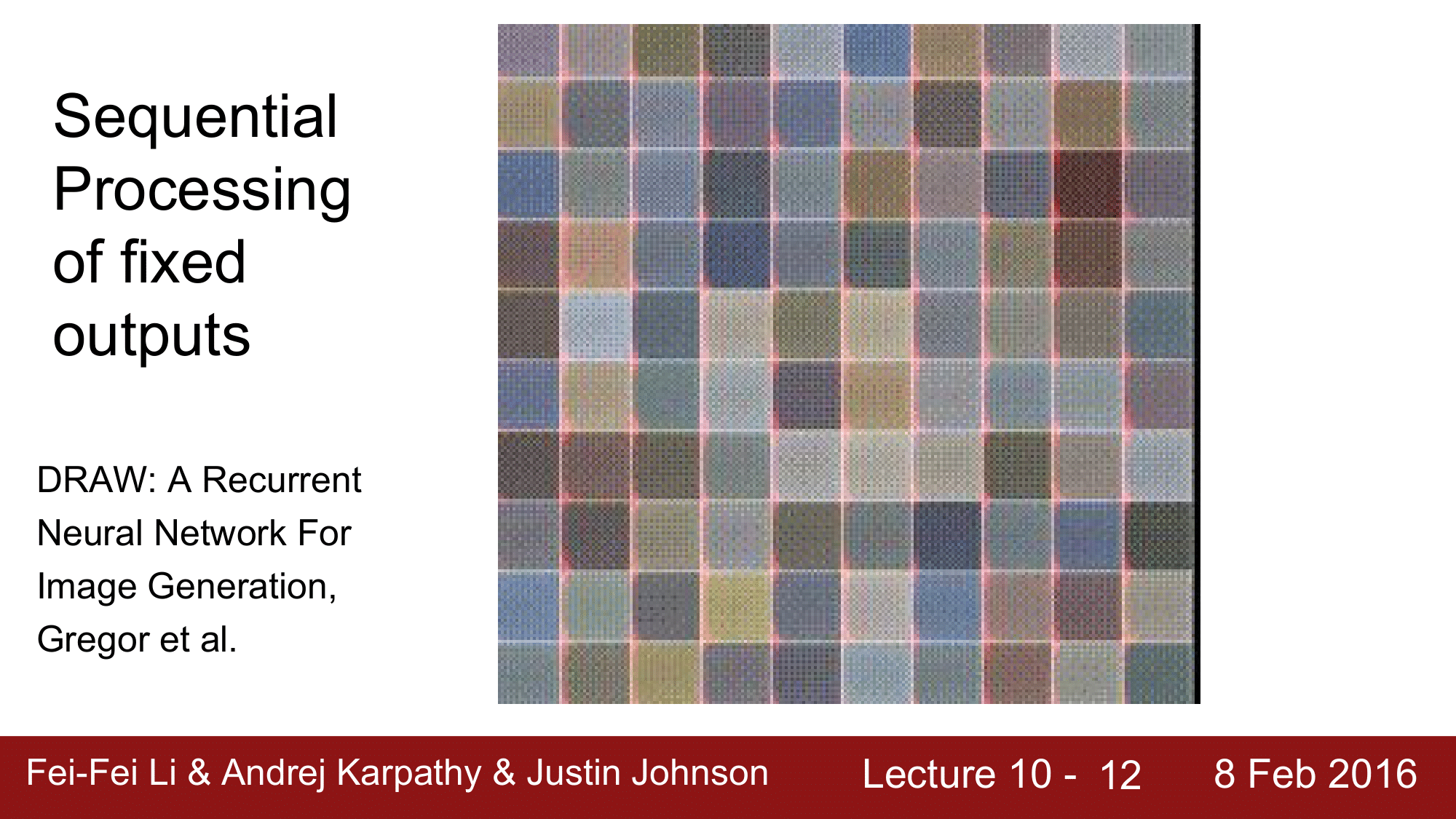
위의 예시는 DRAW 라는 것으로, 앞의 예시와는 반대로 fixed output 을 sequential 하게 처리한 것입니다.
즉, 이것은 output 이기 때문에 무언가를 출력하는 generative model 이라고 할 수 있겠습니다. 영상을 보시게 되면, 한 번에 숫자를 보여주는 것이 아니라 써내려가는 모습을 볼 수 있는데 RNN 에서의 특징을 볼 수 있습니다.
이와 같이, one to one 의 경우에서도 일반적인 CNN 이 아니라 RNN 을 이용해서 분석할 수 있다는 것입니다.
Recurrent Neural Network
지금부터 RNN 의 과정을 상세하게 살펴보겠습니다.
RNN 이 있고, 시간에 따라서 input vector 를 받게 됩니다. 즉, 매 time step 마다 input vector 가 RNN 으로 입력되게 되는데, 이 RNN 은 내부적으로 어떤 상태(state)를 가집니다. 그리고 이 상태를 function 으로 변형해 줄 수 있습니다. 어떤 function 이냐면 매 time-step 마다 input 을 받는 것에 대한 function 으로 만들어 줄 수 있는데, 물론 RNN 도 weight 로 구성이 되며, weight 들이 tunning 되어 가면서 RNN 이 진화하기 때문에 새로운 input 이 들어올 때마다 새로운 반응을 보이게 됩니다.
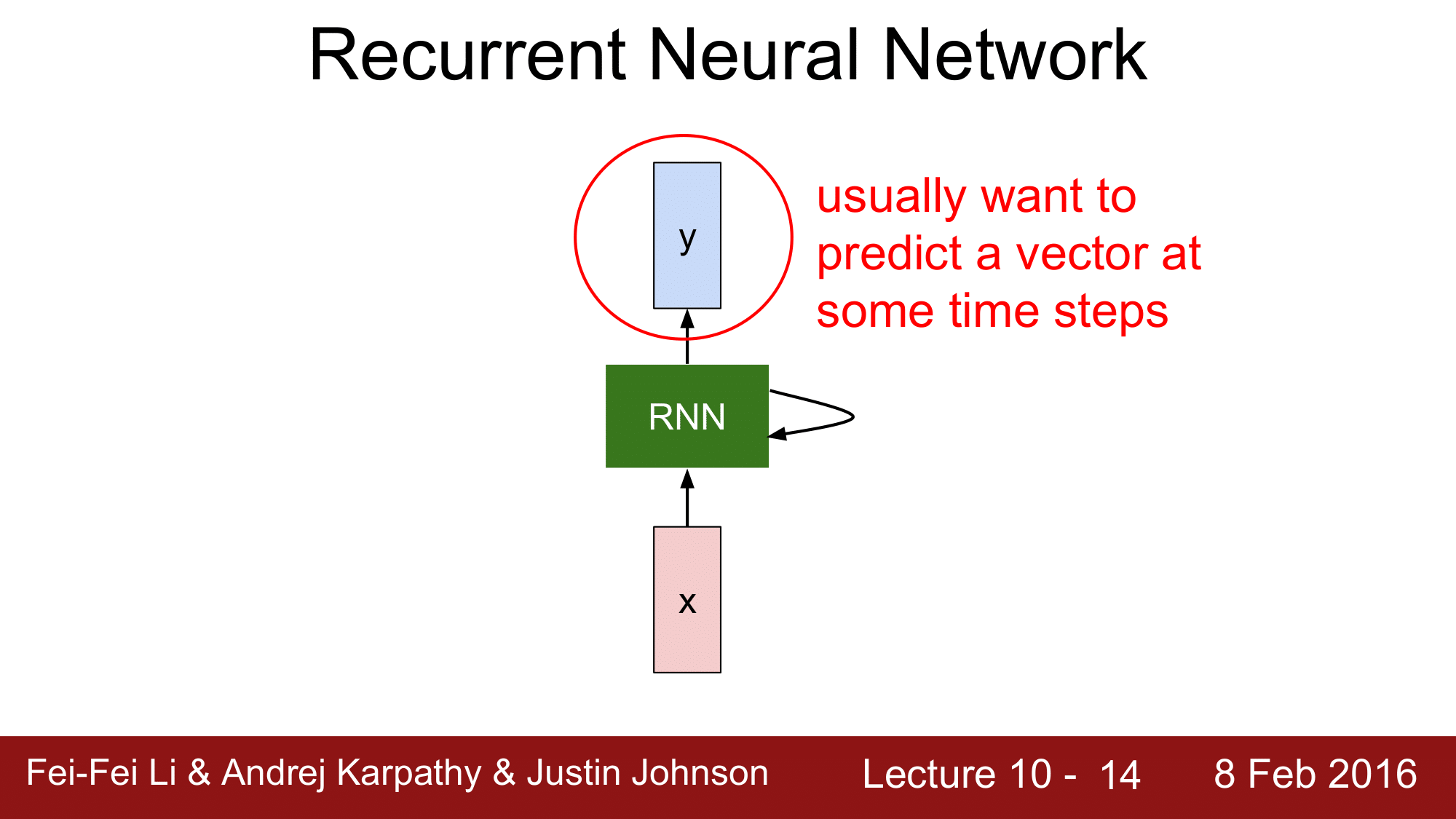
그 이후 특정 time step 에서의 vector 를 예측하길 원하는 것입니다.

매 time step 마다 입력되는 vector x 에 대해서 $h_t = f_W(h_{t-1}, x_t)$ 와 같은 recurrence function 을 적용할 수 있게 됩니다. 이를 적용함으로써 sequence 를 처리해 줄 수 있게 되는 것인데, state 의 update 는 다음과 같이 일어납니다.
새로운 상태(state)를 $h_t$ 라고 하고, $f_W$ 는 파라마터 $W$ 에 대한 function으로 함수의 인자로는 바로 직전의 hidden state 인 $h_{t-1}$ 과 현재 time step 에서의 input vector 인 $x_t$ 가 됩니다.
참고로, 여기에서 state 는 일반적으로 vector 의 collection 으로 표현되고, recurrence function 은 파라미터 W 에 대한 function 이기 때문에 W 를 변경하게 되면 RNN 도 다른 behavior 을 보이게 될 것입니다.
그러므로 RNN 이 우리가 원하는 특정 behavior 를 가질 수 있도록 Weight 값들을 학습시켜나가게 되는 것입니다.

여기서 주의해야 하는 것은 매 time step 마다 동일한 function 과 parameter set 들이 사용되어야 한다는 것입니다. 이렇게 함으로써 RNN 이 input과 output 의 sequence size 에 무관하게 적용이 가능하게 됩니다.
다시 말해, input 과 output 의 sequence size 가 아무리 크더라도 문제가 없다는 의미입니다.
이러한 recurrence function 을 적용한 가장 간단한 사례인 vanilla RNN 에 대해 알아보겠습니다.

vanilla RNN 에서는 상태가 단일의 hidden vector h 로만 구성이 됩니다. 그래서 앞에서 본 대로 현재의 state 는 직전의 state 와 현재의 입력값의 function 으로 표현이 됩니다.
이를 실제의 vanilla state update 로 표현하게 되면 $h_t = \text{tanh}(W_{hh}h_{t-1} + W_{xh}x_t)$가 됩니다. 그래서 $x_t$ 같은 경우 weight 값이 x 에서 hidden layer 로 가는 $W_{xh}$ 의 영향을 받기 때문에 $W_{xh}x_t$가 되고, 직전의 상태 $h_{t-1}$의 경우 현재의 hidden layer 와 직전의 hidden layer 의 영향을 받기 때문에 $W_{hh}$ 를 곱해줍니다. 그리고 이들을 더해 tanh 를 통해 squash 해줌으로써 현재의 state 인 $h_t$를 얻어내게 됩니다. 즉, 현재의 state 라는 것은 history 와 새로운 입력값에 의해서 상태가 변화하게 됩니다.

이해를 돕기 위해 Character-level language model example 이라는 더 구체적인 예시를 살펴보겠습니다.
여기서 학습시키려고 하는 단어는 “hello” 라는 단어로, 이 단어에는 h, e, l, o 라는 4가지의 character 가 들어가 있습니다.
학습을 위해 character 의 sequence 를 RNN 에 feeding 해주고, 매 순간의 time step 에서 RNN 에 다음 step 에 어떤 character 가 올 것인지를 예측하게 합니다.
예를 들어, h 를 넣으면 그다음 step 으로는 e 가 나오게 된다는 것을 예측하게 합니다. 이렇게 한 step 씩 진행하면서 전체적인 distribution 을 예측하는 것입니다.
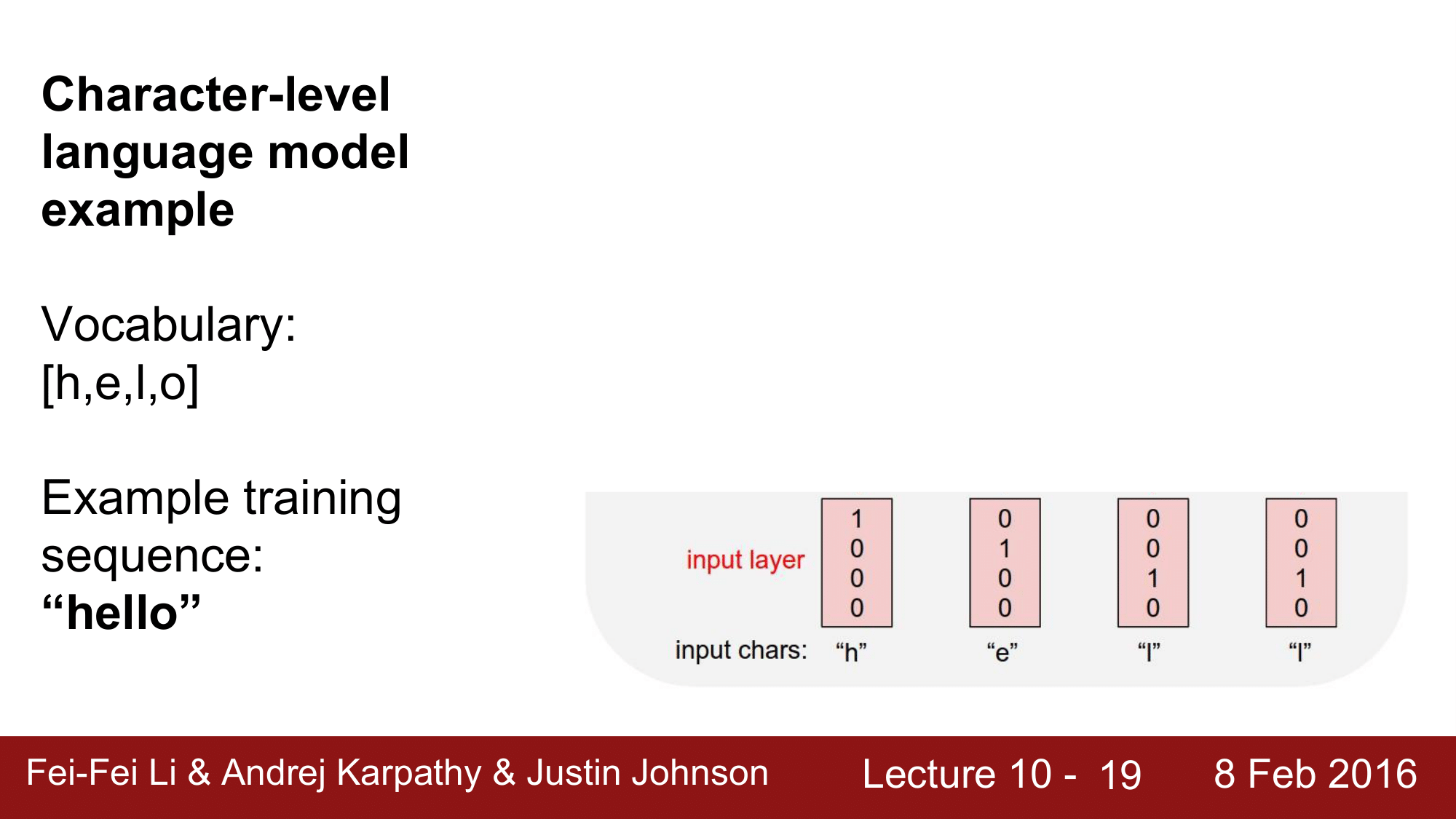
RNN 에 feeding 을 해줄 때는 위의 input [h, e, l, o] 를 one-hot encoding을 합니다.
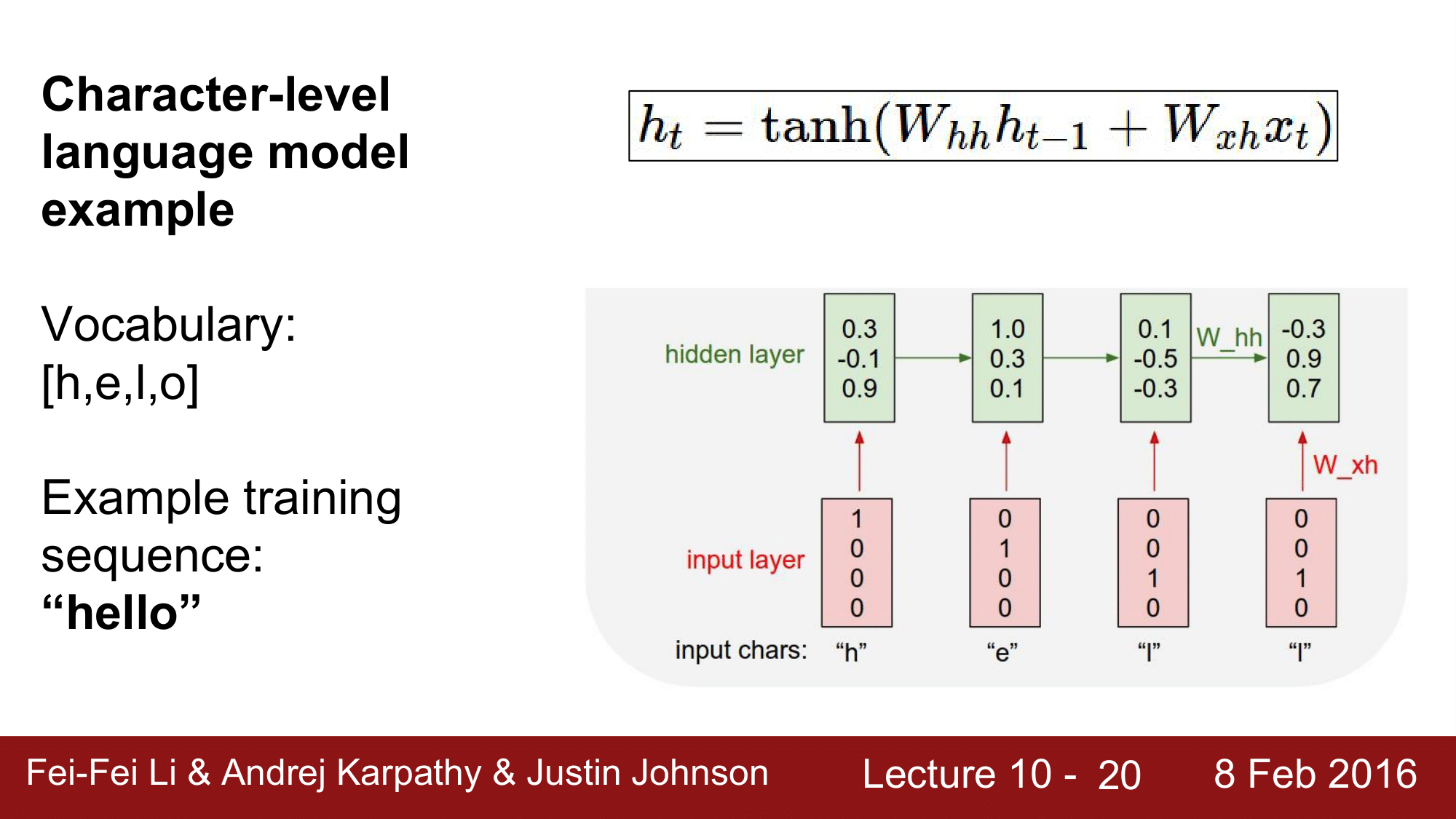
hidden layer는 일단 임의의 값으로 초기화한 뒤, 입력을 받고 hidden layer 를 통해 어떤 출력값을 도출합니다. 그리고 hidden layer 는 다음 layer 로 영향을 주게 됩니다. 이렇게 이동하는 것을 $W_{hh}$ 라고 하고, input layer 에서 hidden layer 로 이동하는 것을 $W_{xh}$ 라고 합니다.
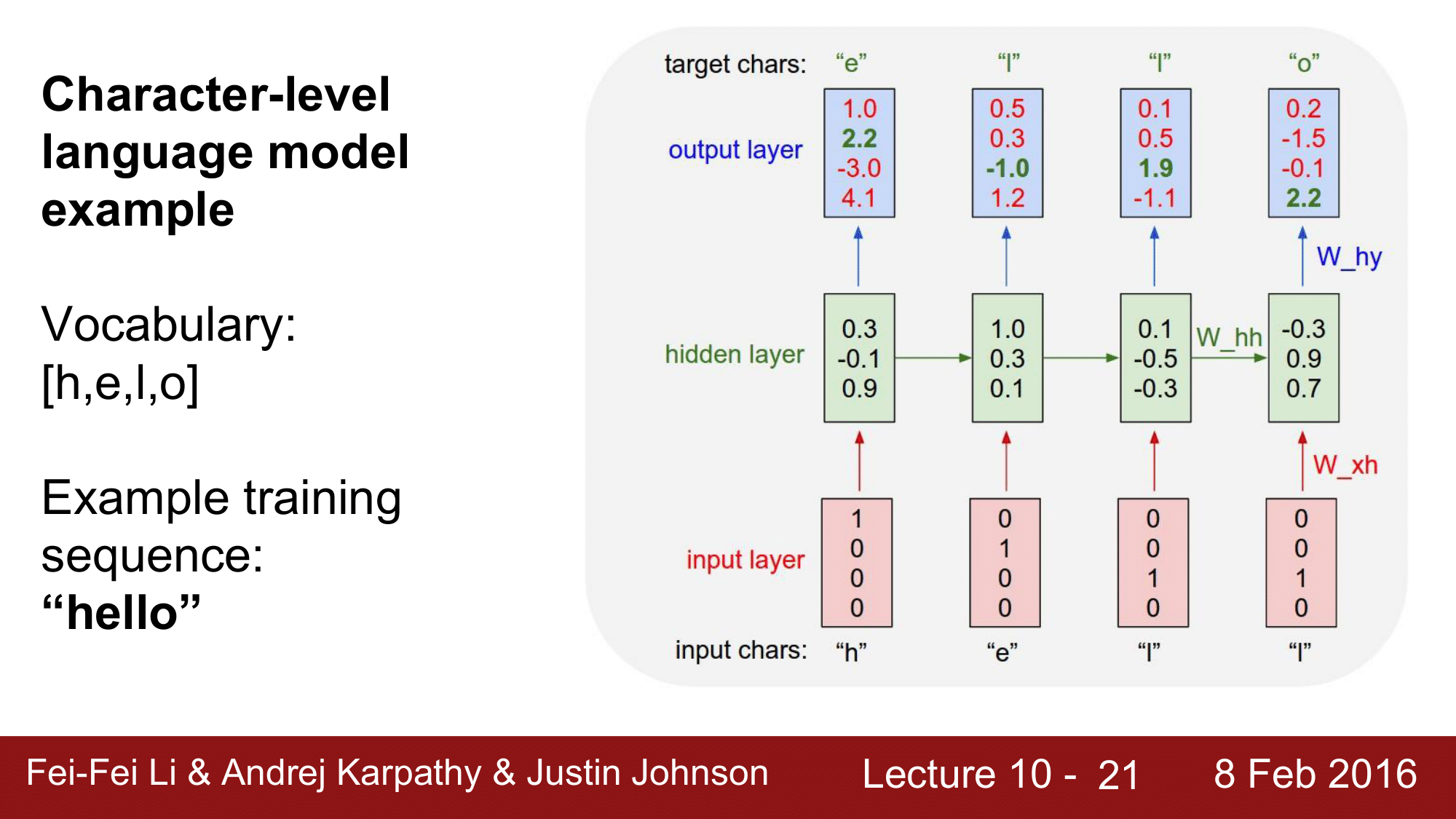
output layer 는 input layer 와 마찬가지로, 4개의 character 에 대한 array 로 represent 한 결과를 도출합니다.
첫 번째 레이어의 경우, e 에 해당하는 값을 2.2 로 output 을 도출한 것이고, 뒤단의 레이어들의 경우 l은 -1.0, 1.9, o는 2.2 로 예측한 것을 볼 수 있습니다.
정답에 해당하는 값은 e, l, l, o 인데 예측값은 o, o, l, o 가 나온 것을 확인 할 수 있습니다. 이런 식으로 오차가 발생하는 것을 확인할 수 있는데, 이러한 오차를 이용하여 loss 를 구해 다시 아래쪽으로 backpropagation 을 해줍니다. 이를 통해서, gradient 를 수정해나가며 계속해서 학습을 진행하게 됩니다.
물론, 각각의 time step 에는 softmax classifier 가 존재합니다. 이를 이용하여 loss 를 계산하게 됩니다. 그리고 또 한 가지 기억해야 하는 것은 W_xh, W_hh, W_hy 가 위 그림에서 여러 번씩 화살표로 사용되고 있는데, 처음 RNN 을 들어가면서 모든 time step 에서 동일한 recurrence function 과 동일한 parameter 가 사용된다고 했습니다. 그래서 각각의 과정(화살표)에서 다른 W 가 사용되는 것이 아니라 동일한 것이 사용된다는 것을 반드시 기억해야 합니다.
이런 식으로 처리함으로써 input 과 output 의 sequence에 상관없이 처리가 가능하다는 것입니다.
좀 더 이해를 높이기 위해 코드를 살펴보겠습니다.

이런 식으로 character-level 의 RNN 은 python 기반의 numpy 를 이용하여 불과 112줄의 코드로 구현이 가능한 것입니다.
이를 좀 더 자세히 들여다보겠습니다.

코드의 첫 번째 부분인 Data I/O 부분을 보면, numpy 를 import 하고 data 를 불러와 유니크한 character 를 저장하게 됩니다.
여기서 중요한 부분은 char 와 index 를 연관시켜주었다는 것인데, char_to_ix와 ix_to_char 를 이용하여 mapping 시켜 주었다는 점 입니다.

Initialization 에서는 hyperparameter 를 설정하고 weight 와 bias 를 설정해줍니다.
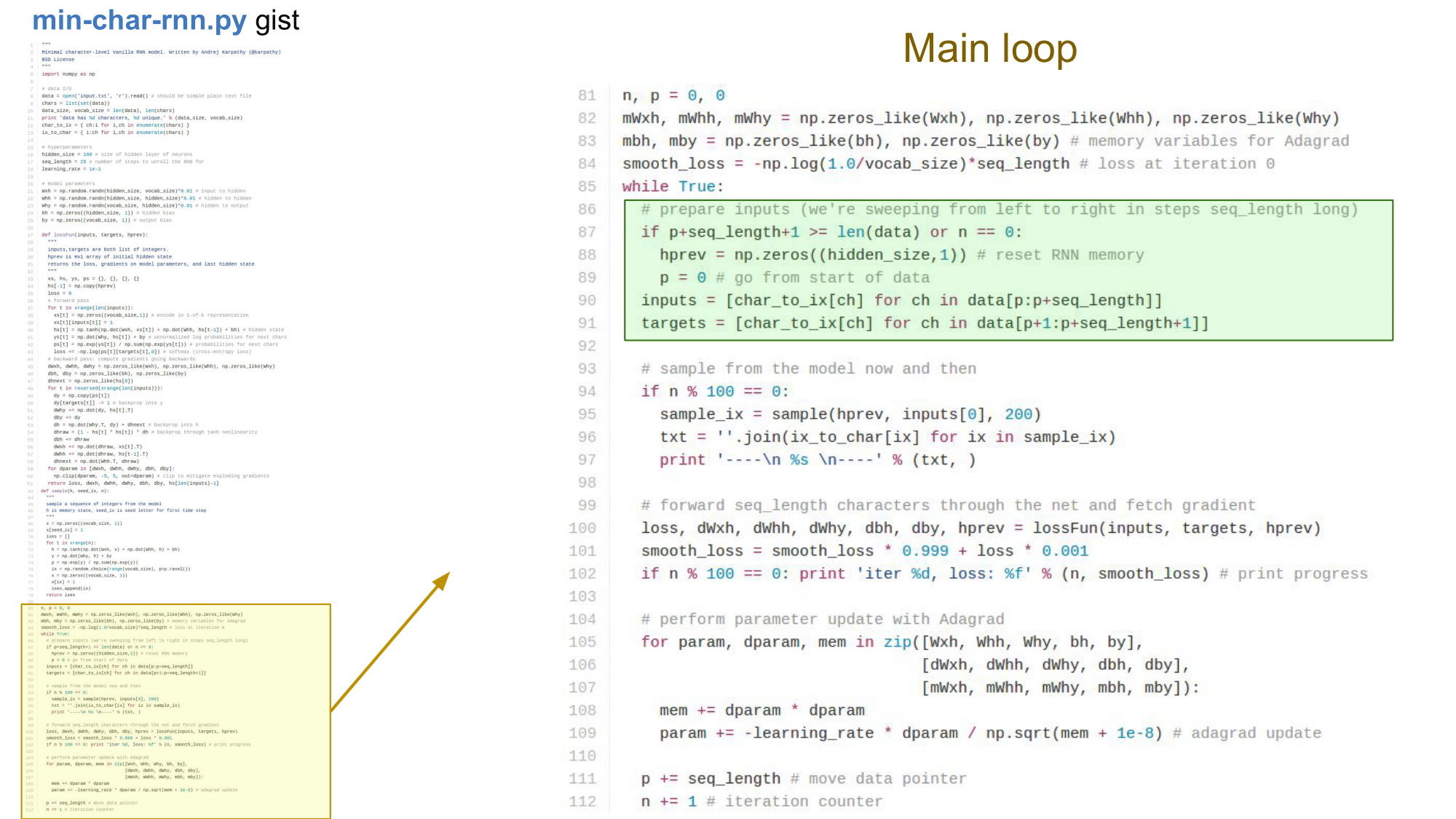
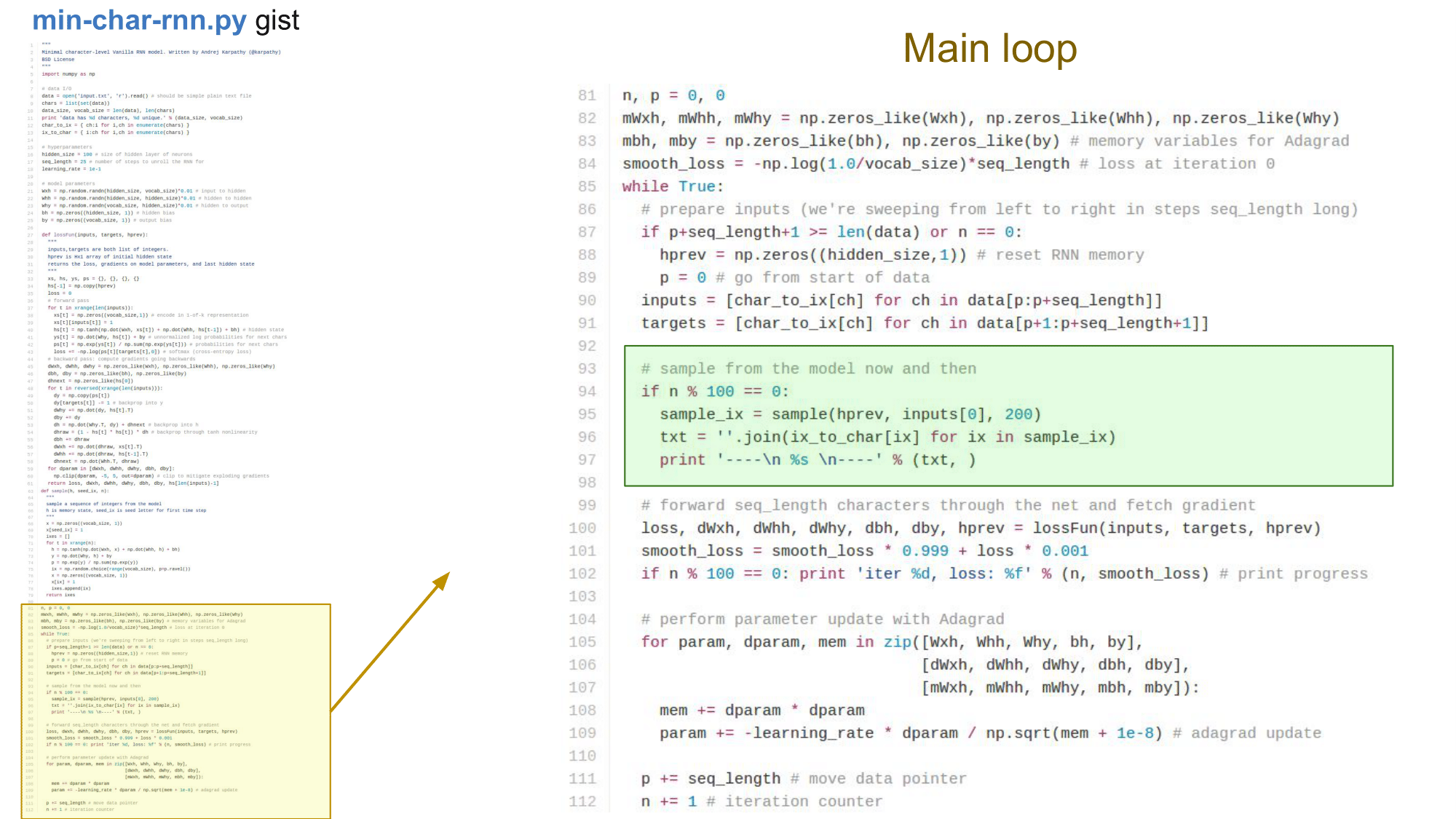
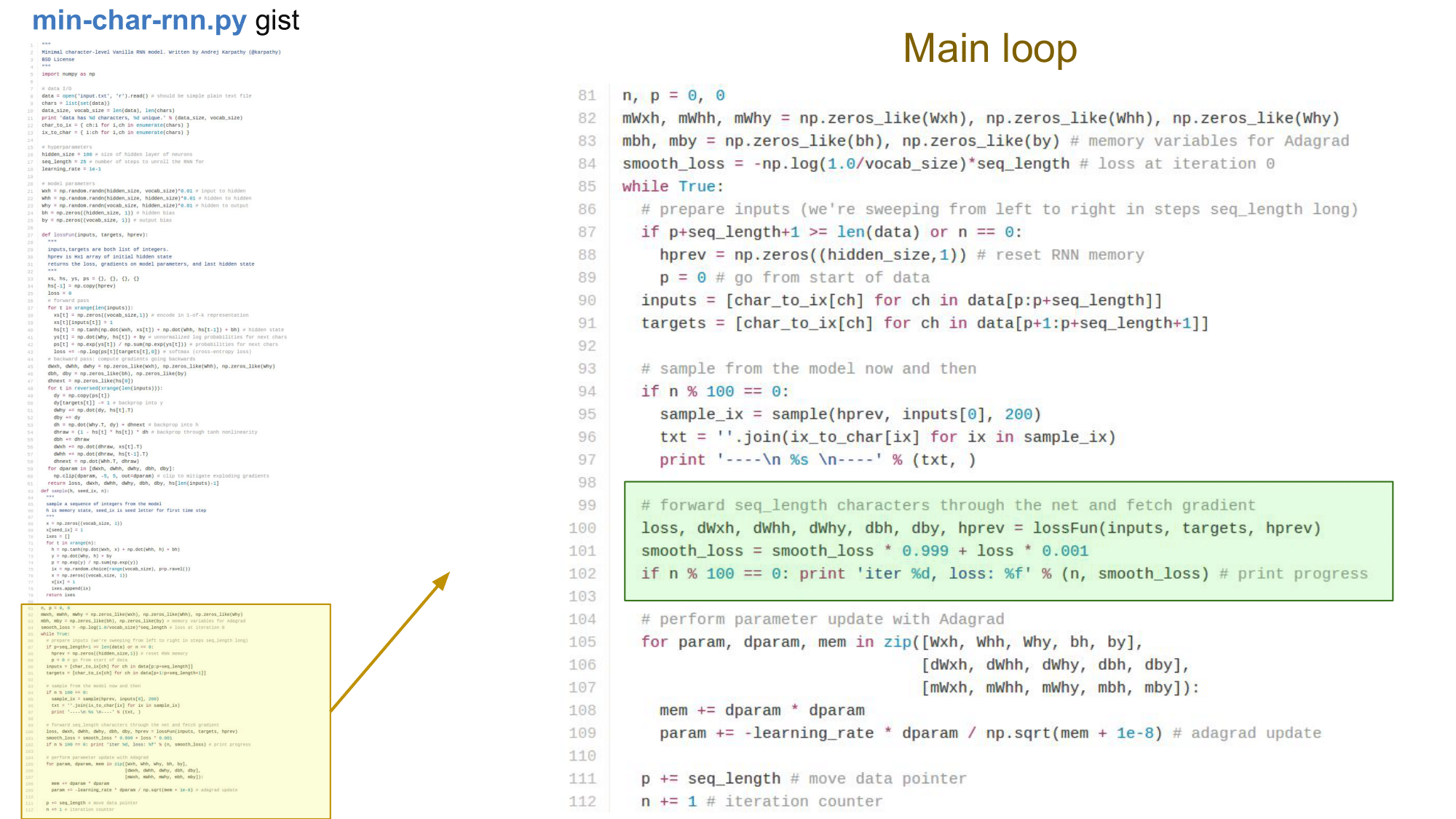
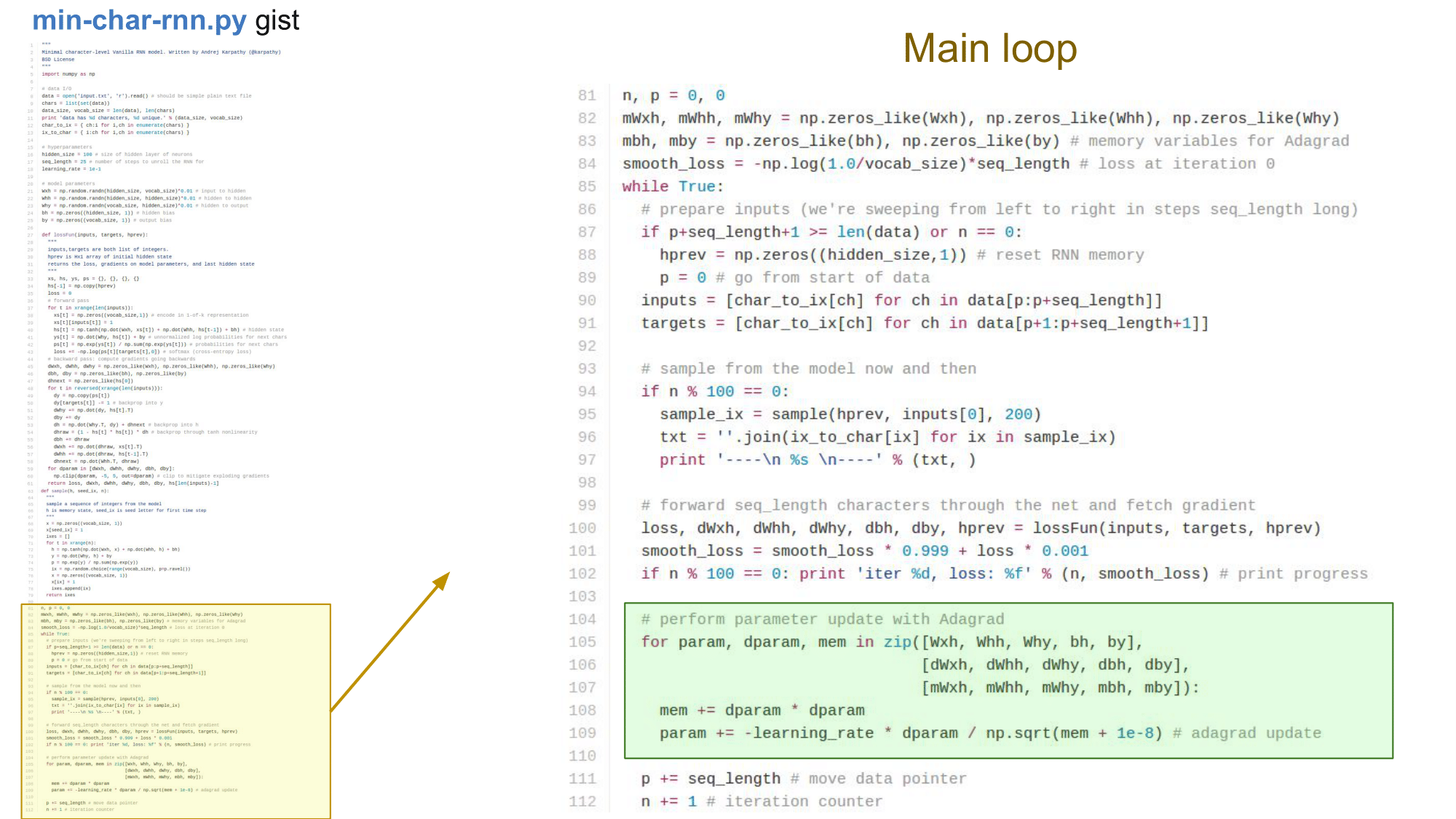
Main loop

Loss function

softmax
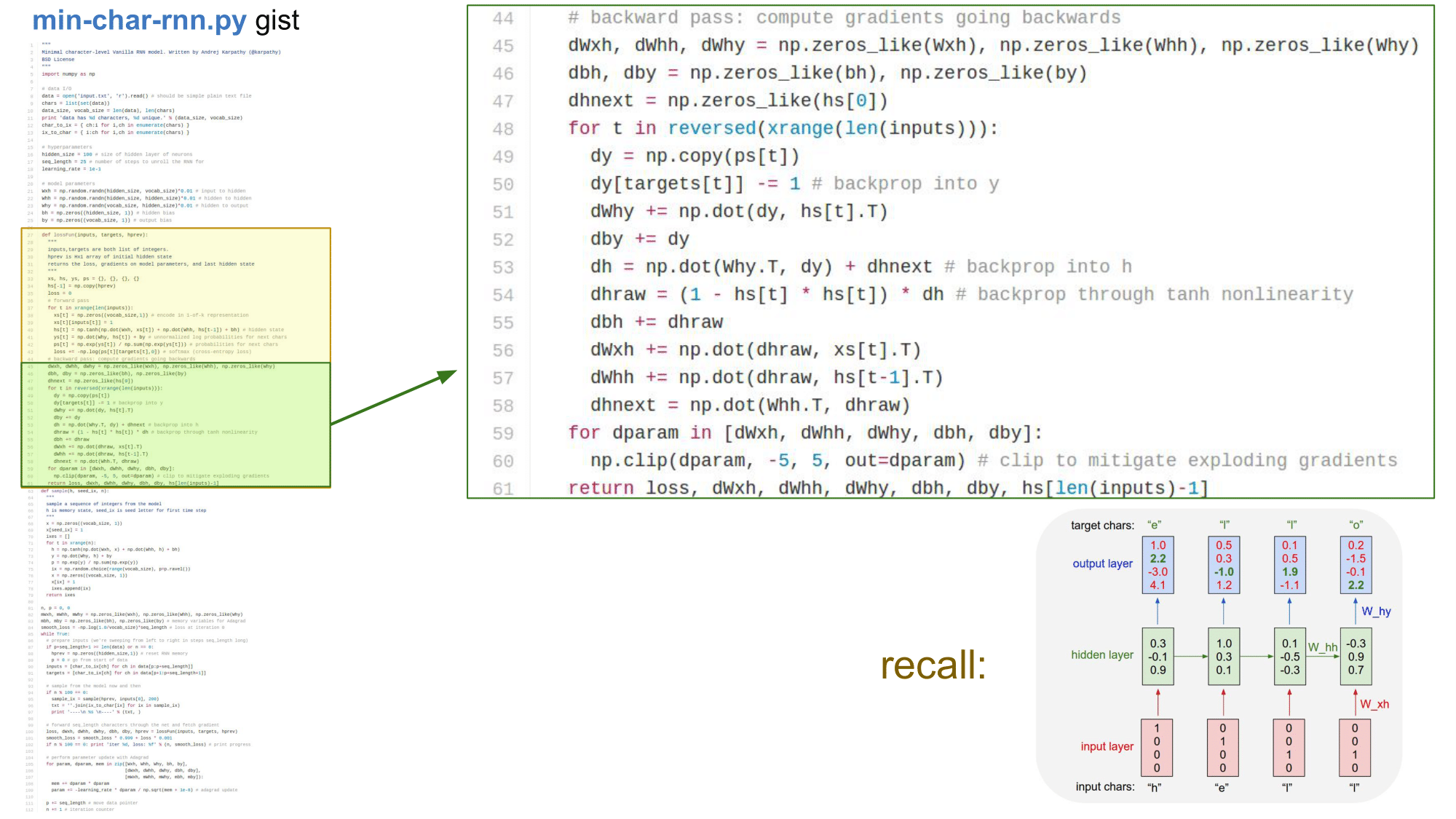
backprop
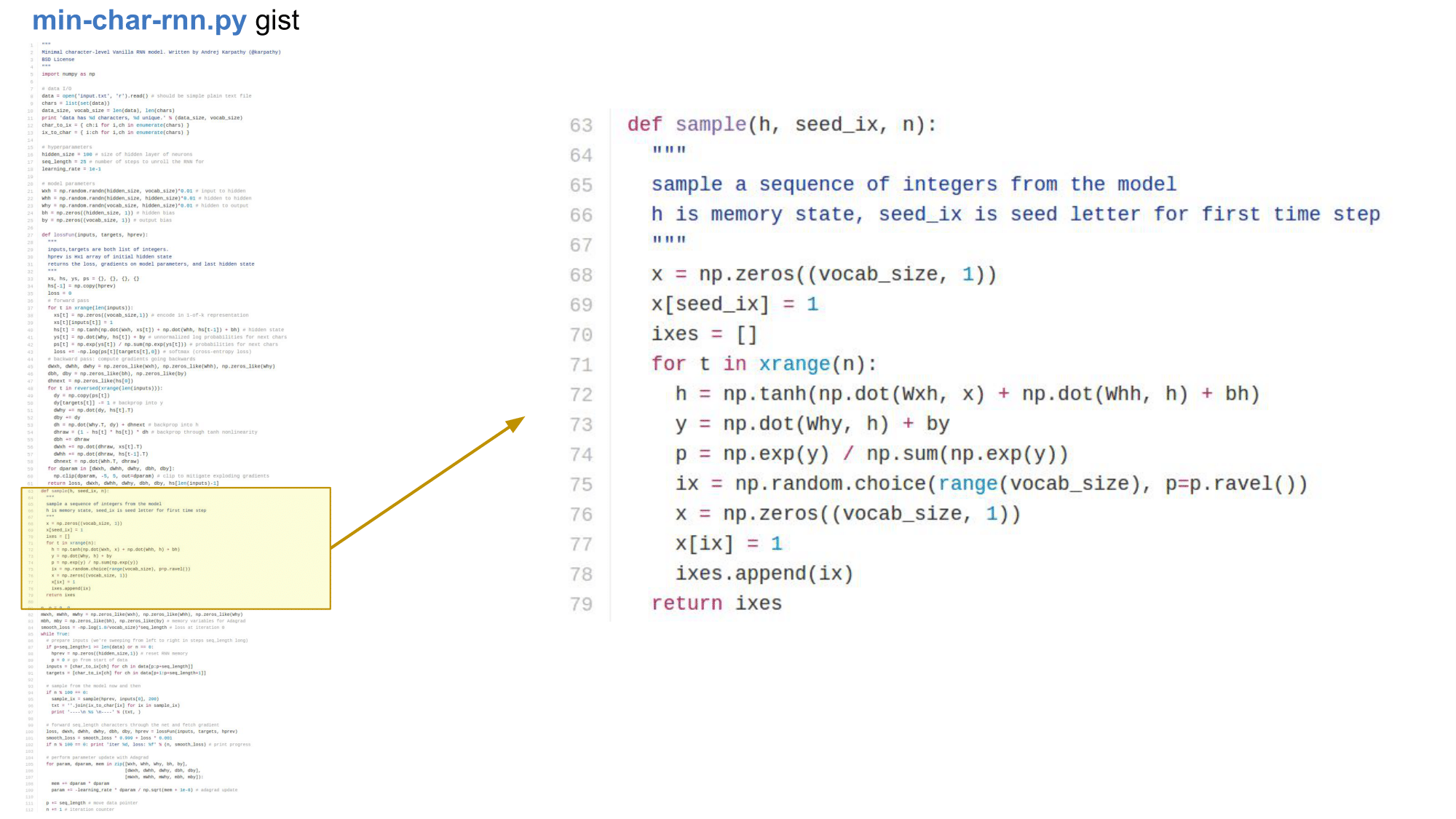
sample
이 정도의 간단한 코드로 많은 일을 할 수 있습니다.
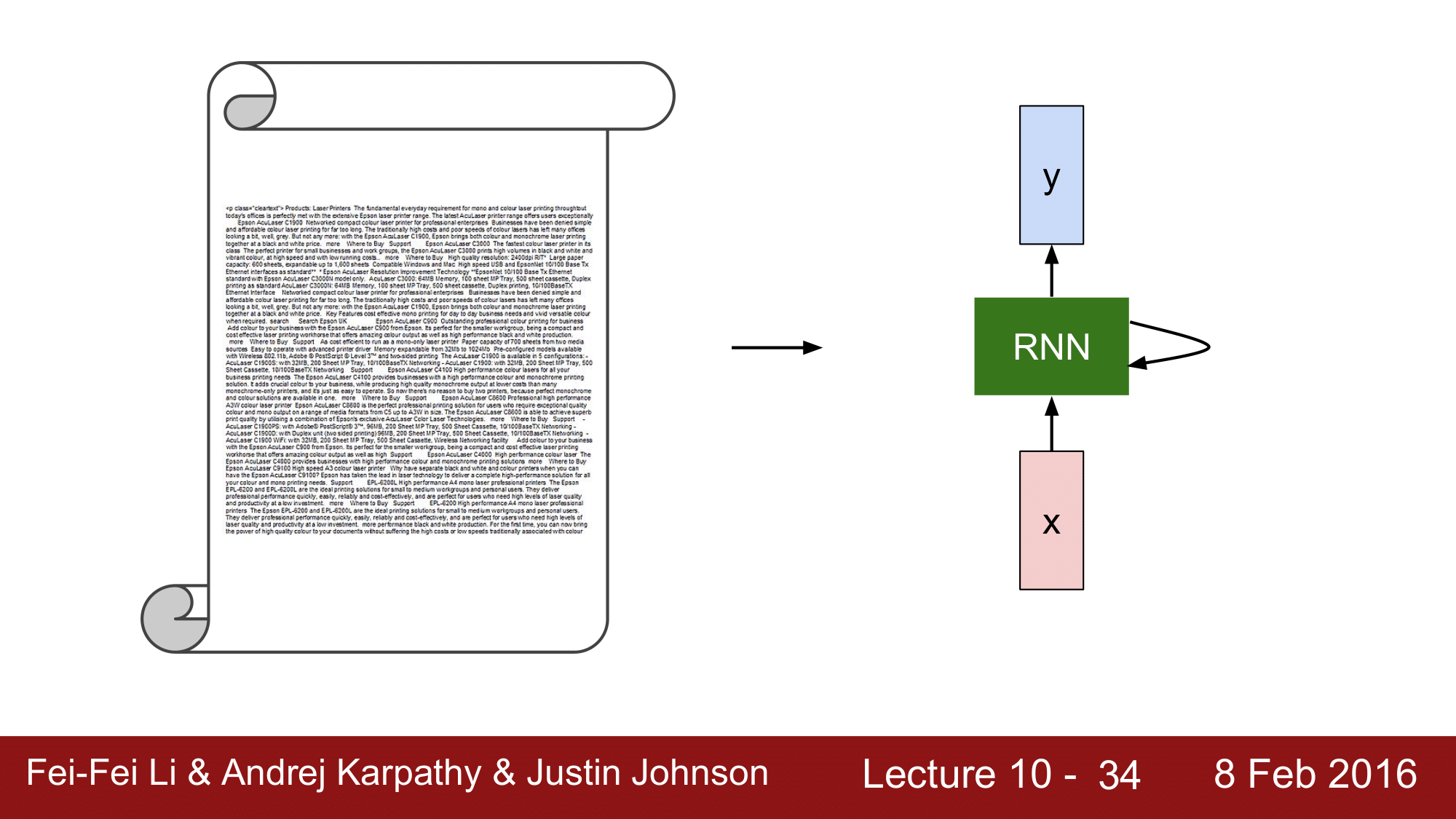
하나의 예로, 굉장히 긴 문장을 RNN 에 넣어서 Regenerate 하는 것을 살펴보겠습니다.

input 으로 셰익스피어의 작품을 넣어보게 되면 다음과 같이 됩니다.

처음 step 에서는 알아볼 수 없는 문장이 나오지만, 학습을 반복하면서 그럴싸한 문장이 생성되는 것을 볼 수 있습니다.

최종적으로는 위와 같은 문장을 만들었는데, 얼핏 보면 굉장히 있어 보이는 문장이 나오게 됩니다.
이 외에도 LATEX 나 LINUX 를 학습시켜서 다음과 같이 그럴싸한 결과물들을 뽑아내는 것을 볼 수 있습니다.
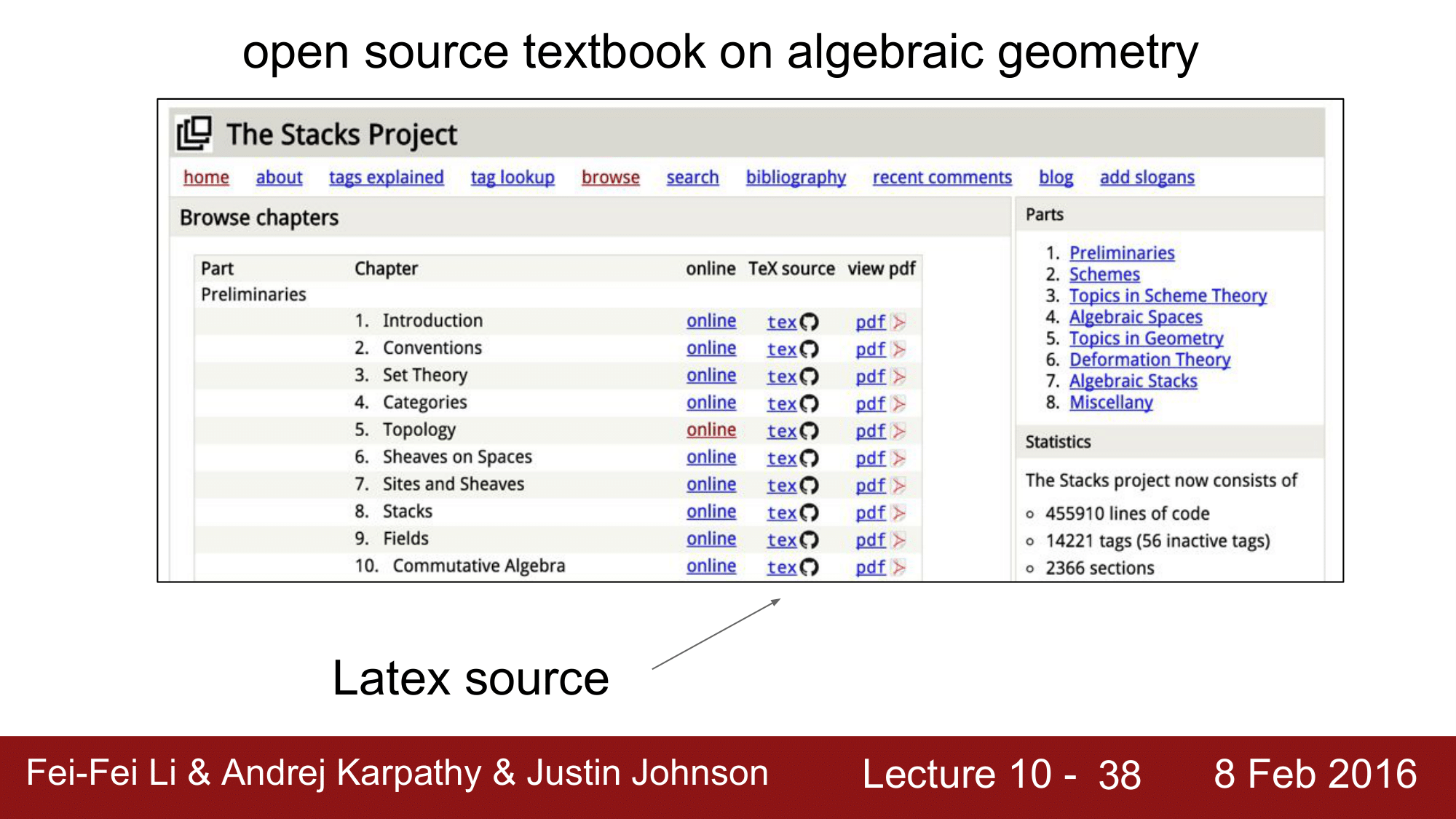


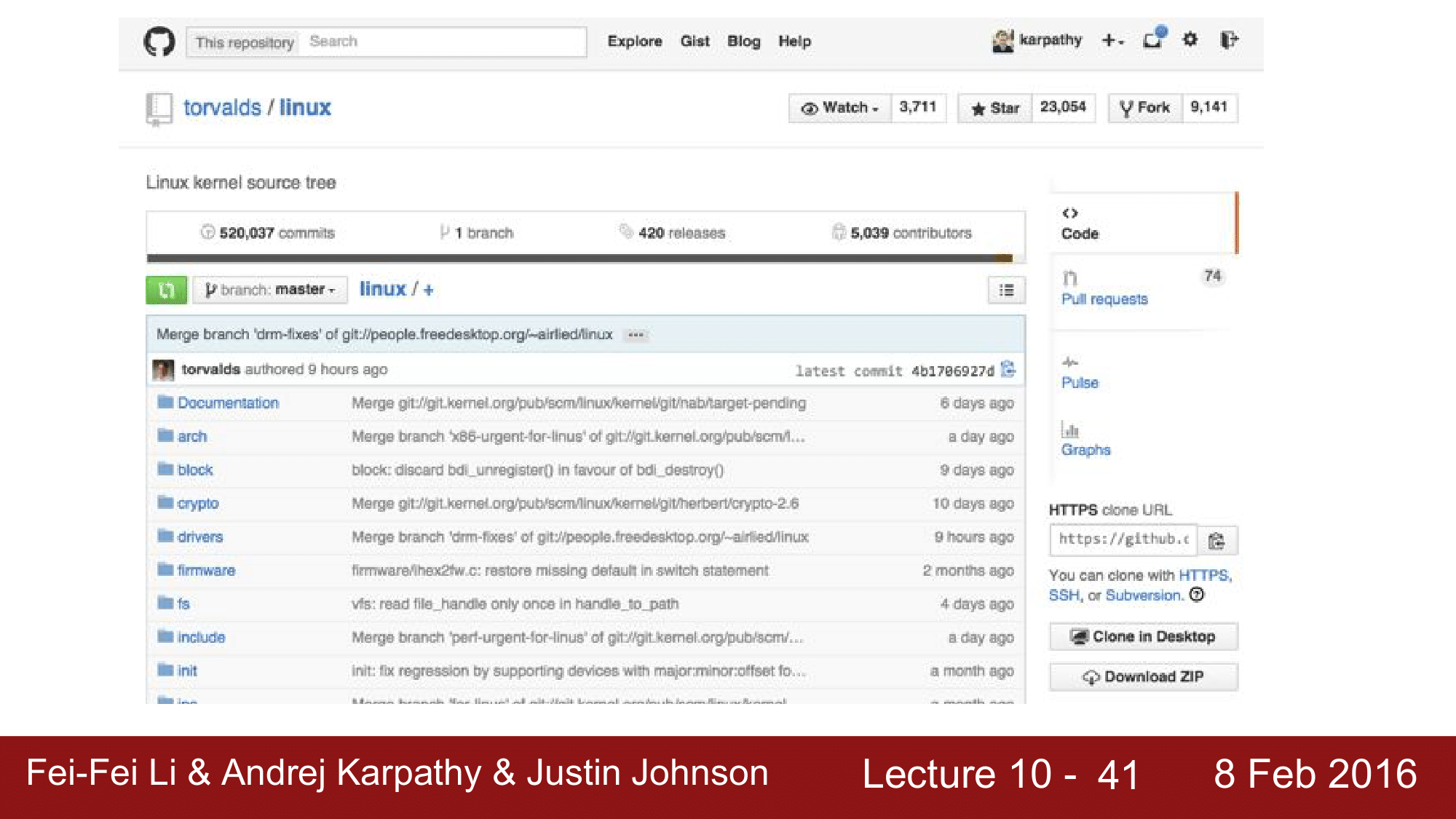



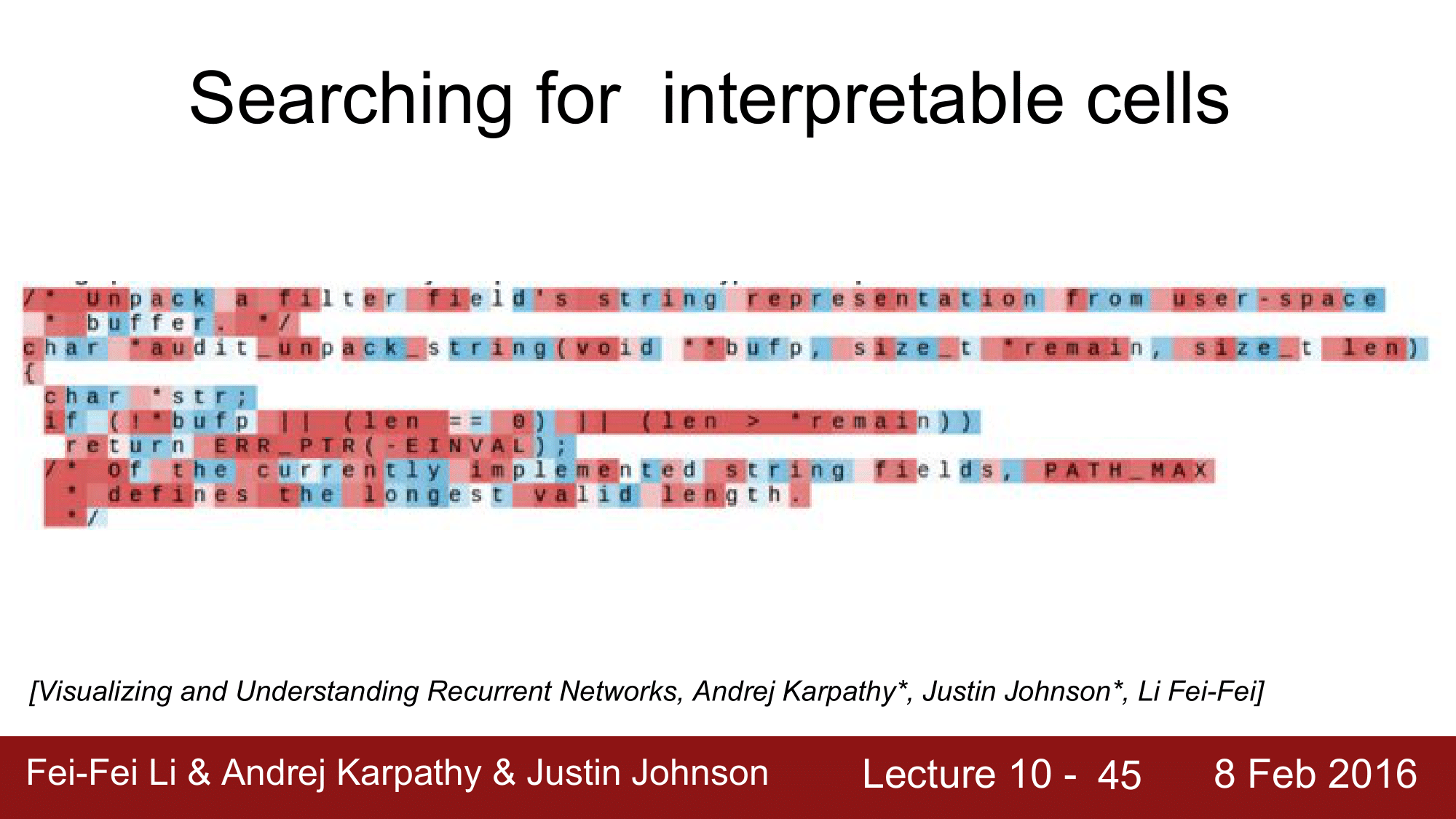
다른 실험으로 각 셀들이 어디를 관찰하고 있는지를 찾아본 것이 있습니다. 결론적으로, RNN 에서 hidden state vector 내의 cell 을 들여다보니, 그 cell 이 어떤 면에 대해서 excited 된다는 것을 발견했습니다.
물론 모든 cell 이 이런 규칙을 갖고 있다는 것은 아니지만, 약 5%의 cell 들이 그러하다는 것입니다.

그 첫 번째 예로, quote detection cell 입니다. 여기서 주목할 점은 seq_length 를 100으로 줬음에도 불구하고 100자가 넘은 범위에 대해 quote 를 검출했다는 점입니다. 이에 대해서는 전 단계의 hidden state vector 의 상태를 넘겨주고, 100자를 넘어가지만 generalize 하는 방식으로 인식하는 것 같다고 설명합니다.

위의 예시는 톨스토이의 전쟁과 평화를 학습시킨 것인데, 여기서 특정 셀은 하나의 line 에 대한 것만 tracking 하는 것을 확인할 수 있습니다.

다음으로는 if statement 를 검출하는 cell 있고,
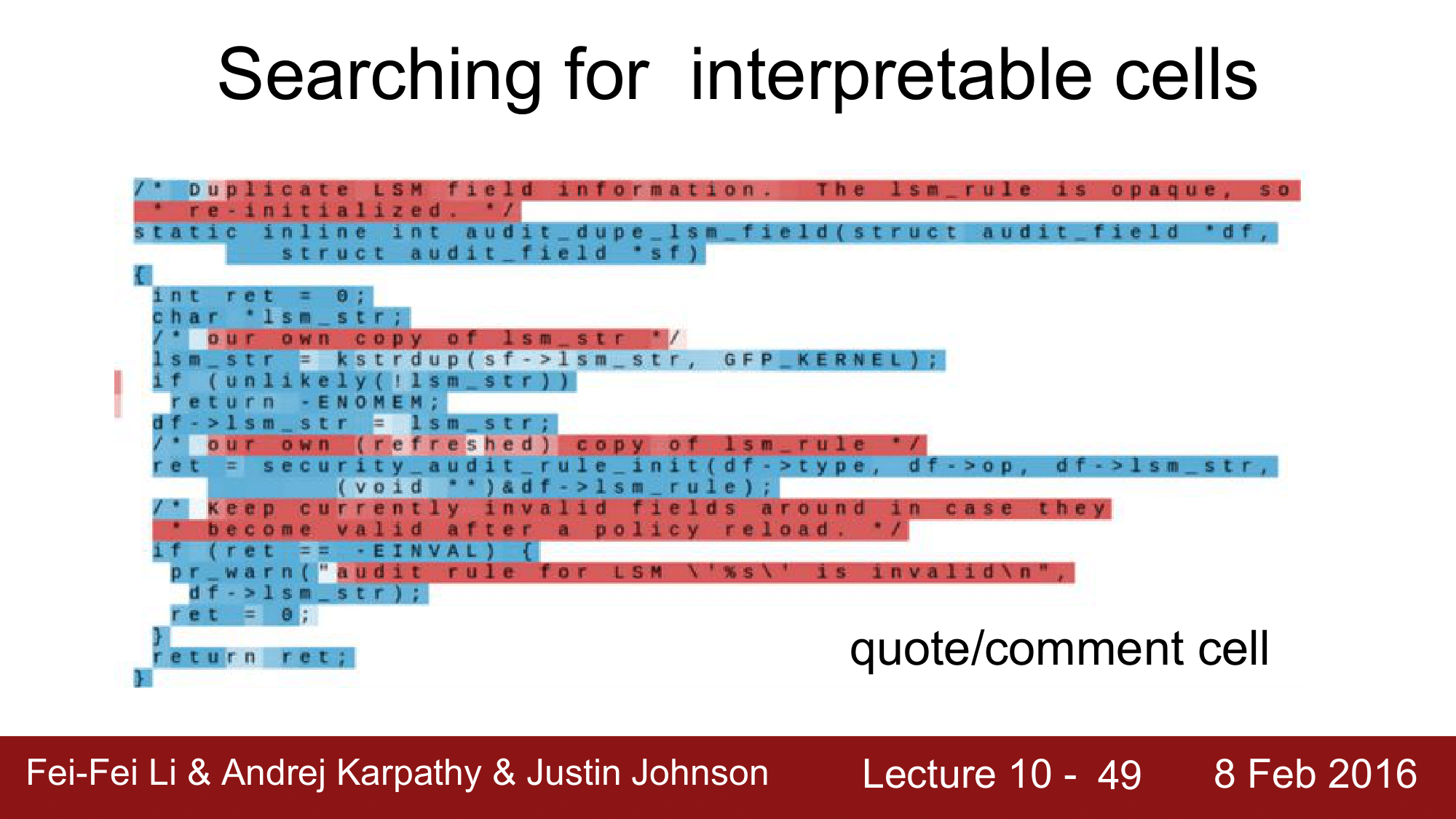
quote 와 comment 를 검출하는 cell

code 의 depth 를 검출하는 cell 등이 되겠습니다.

RNN 을 잘 활용한 또 하나의 예시는 Image Captioning 이 되겠습니다.
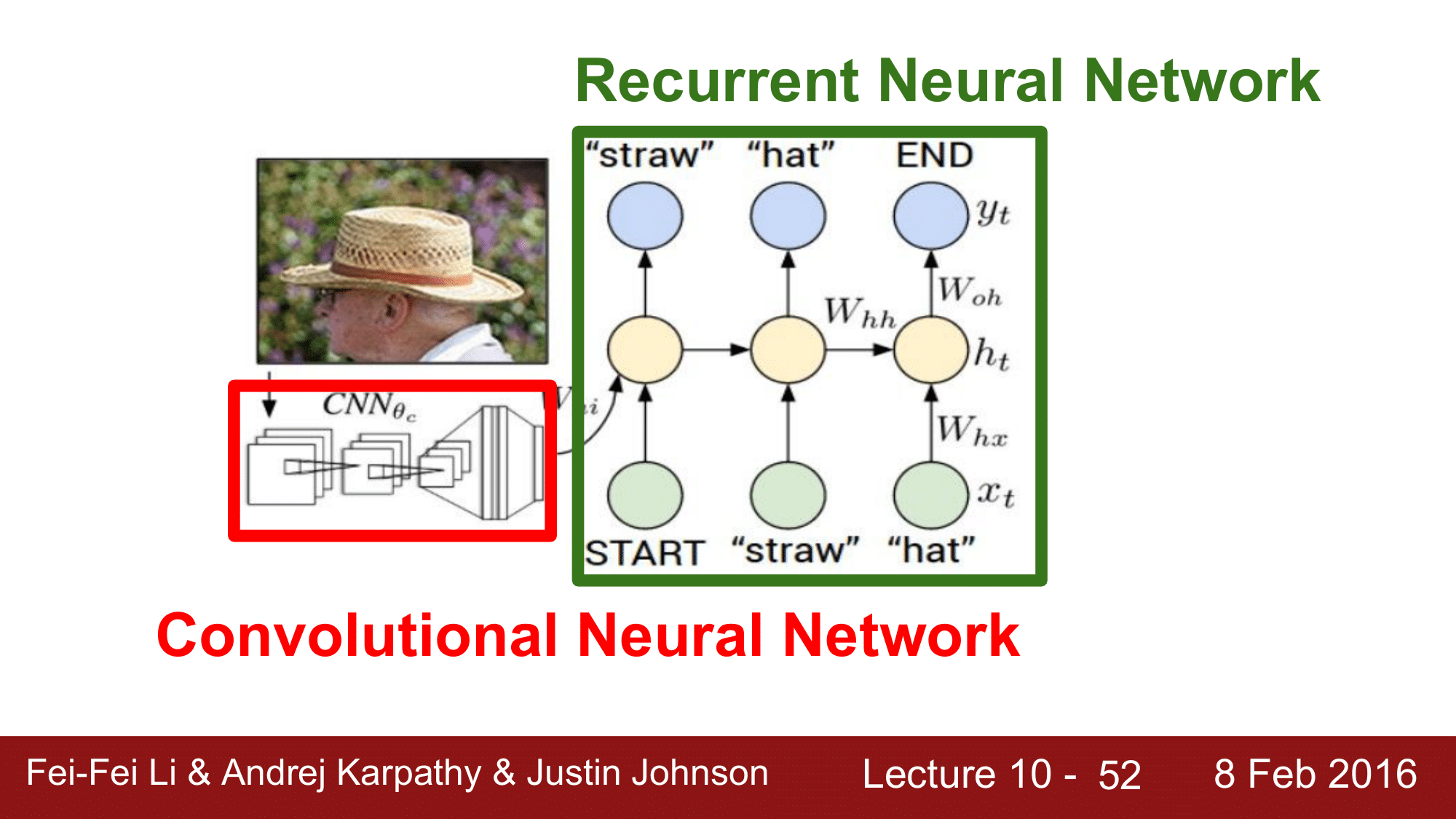
Image Captioning 은 두 개의 module 로 이루어집니다.
첫 번째는 Convolutional Neural Network, 두 번째는 Recurrent Neural Network 가 되겠습니다.
CNN 에서는 이미지를 처리해 주고, RNN에서는 시퀀스를 처리해 주게 됩니다. 즉, 위의 화살표대로 CNN 의 결과물을 다시 입력값으로 받아서 출력해 주는 generative 한 프로세스가 되겠습니다.
이 단계를 상세하게 살펴보면 다음과 같습니다.

먼저 테스트 이미지를 받고,

테스트 이미지를 CNN 에 feed 해줍니다.
Conv. Net 으로는 VGG NET 을 활용하고 있는 예시입니다.

layer 의 끝을 보게 되면, FC 와 softmax 가 있는데 이 2개의 layer 를 없애버립니다.
이렇게 해서 없애버린 부분이 CONV NET 의 top 부분이 되고, 이 부분을 RNN 쪽으로 보내주게 됩니다.

RNN 으로 보내주기 위해 일단 special 한 START vector 를 처음 시작할 때 꽂아 줍니다.
여기서 START vector 의 역할은 RNN 에게 시퀀스가 시작된다는 것을 알리는 것으로, 최초 iteration 시에 꽂아주게 됩니다.
그리고 여기에서 CNN 부분과 RNN 부분의 경계는 두 모형 사이가 될 것입니다.
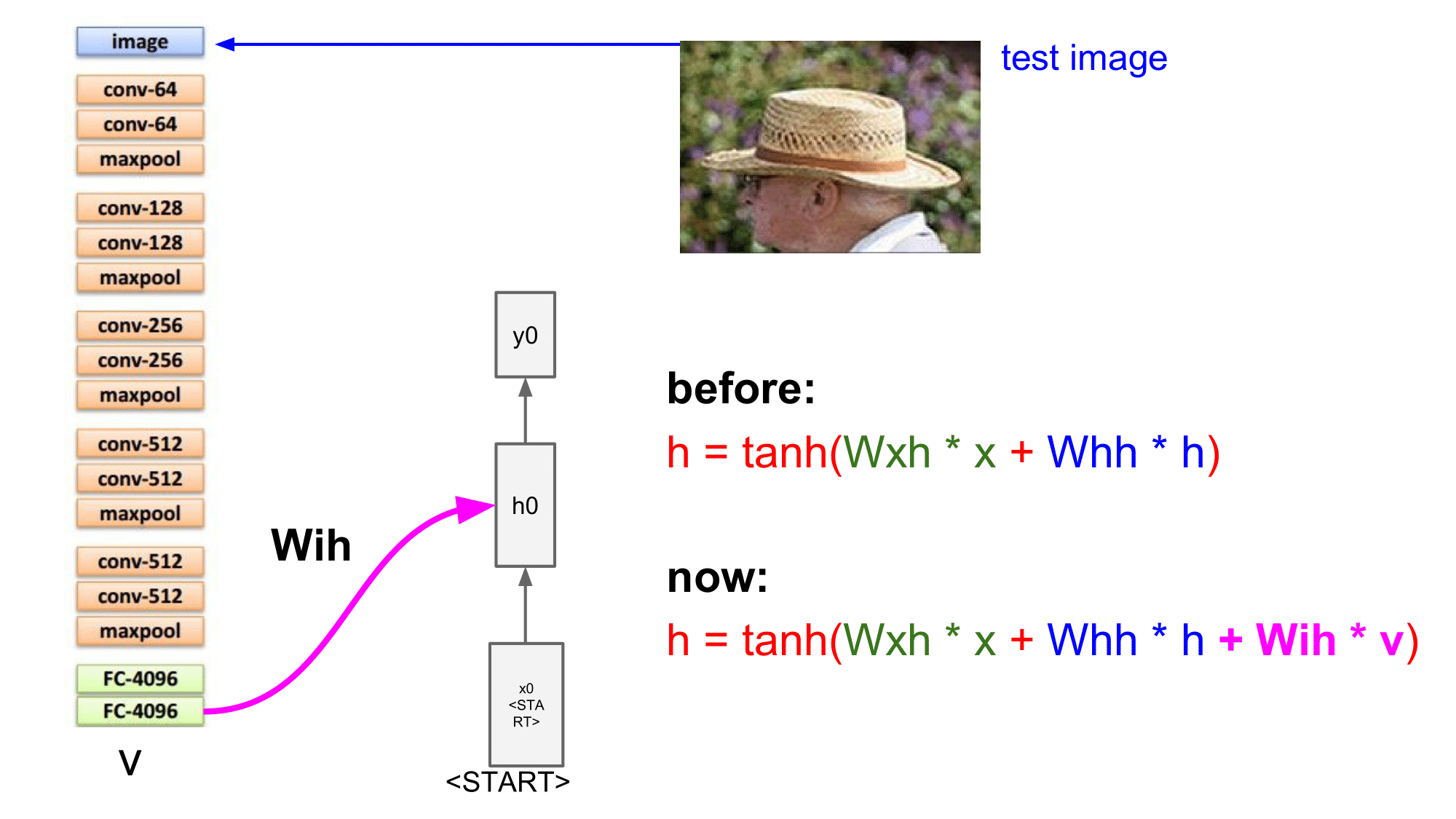
기본적으로 RNN 은 앞에서 알아본 대로, Wxh 부분과 Whh 부분, 두 가지를 더해주어 tanh 로 squash 한 것이 hidden state 이었는데, Image Captioning 에서는 Wih * v 가 추가됩니다.
Wih 는 image 에서 hidden 으로 가는 부분이고, v 는 top of the conv net 의 값이 됩니다.
이 두 값을 곱해준 값을 더해주게 되면 어떻게 되는지 알아보겠습니다.
위 test image 는 할아버지가 밀짚모자를 쓰고 있는 이미지로 CNN 의 input 으로 들어오게 되면, CNN 이 straw 를 인식하게 됩니다. 이 인식의 결과가 Wih 를 통해서 h0 의 상태에 영향을 주게 됩니다. 즉, straw 라는 단어의 확률이 높아지도록 영향을 주게 됩니다.
이후, h0에서 y0으로 전달이 되면 y0에서의 straw 와 관련된 수치가 높아지게 됩니다.
이러한 방식으로 Wih 가 RNN 에 영향을 미치게 됩니다.
그러므로 Image Captioning 에서 RNN 은 두 가지 업무를 수행하게 됩니다.
첫 번째는 기존에 설명했던 것처럼 다음 단어를 예측하는 일이고, 두 번째는 이미지 정보를 기억하는 일을 곡예하듯이 진행하게 됩니다.
참고로 Whh 같은 경우는 전 단계가 없기 때문에, 최초에는 0이 됩니다.
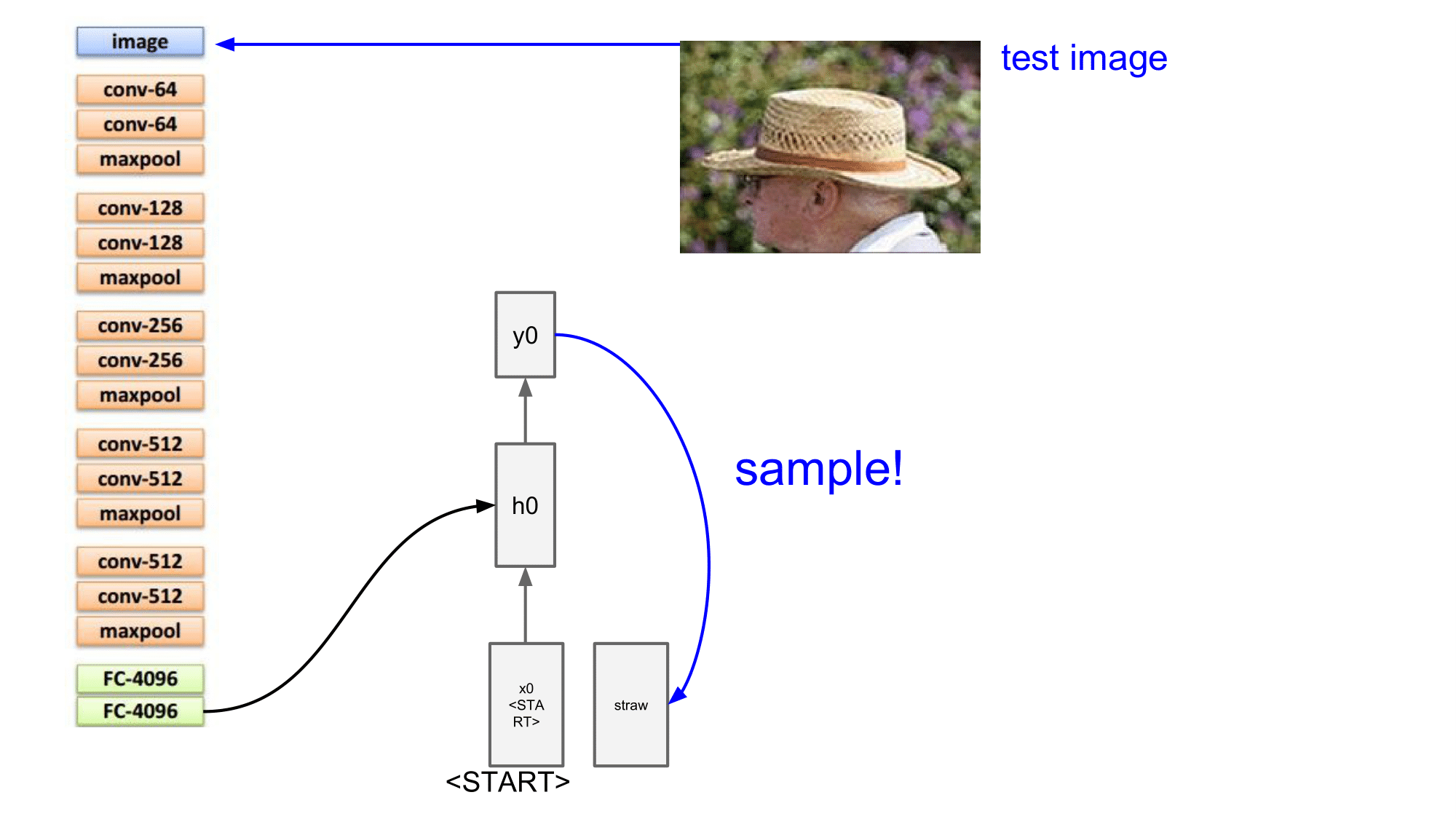
CNN 이 straw 를 잘 classify 하게 되면 Wih 가 RNN 에 영향을 많이 주고, 잘 된 경우 straw 라는 단어가 RNN 의 다음 step 에서 input으로 쓰이게 됩니다.
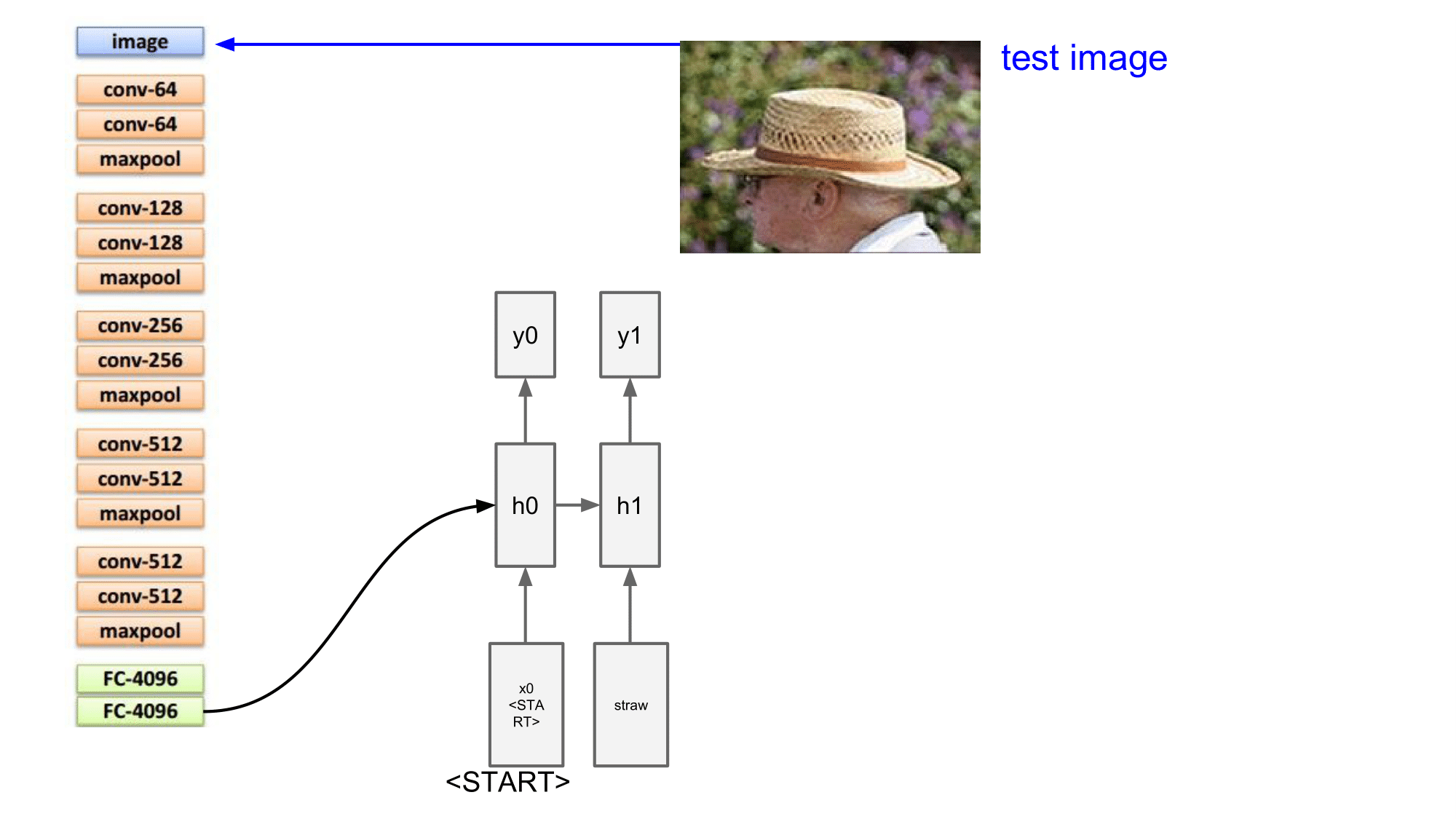
그리고 그다음 step 에서는 h1, y1 으로 전달되게 되는데, 여기에서는 straw 말고 hat 이라는 것을 인식했다고 했을 때 Wih 를 통해 h0 h1 을 거치게 되면 y1 에 영향을 주게 됩니다. 그리고 그 영향이 충분히 컸다고 한다면, 다음과 같이 hat 이 sampling 이 되어 다음 step 의 input 으로 들어오게 될 것입니다.
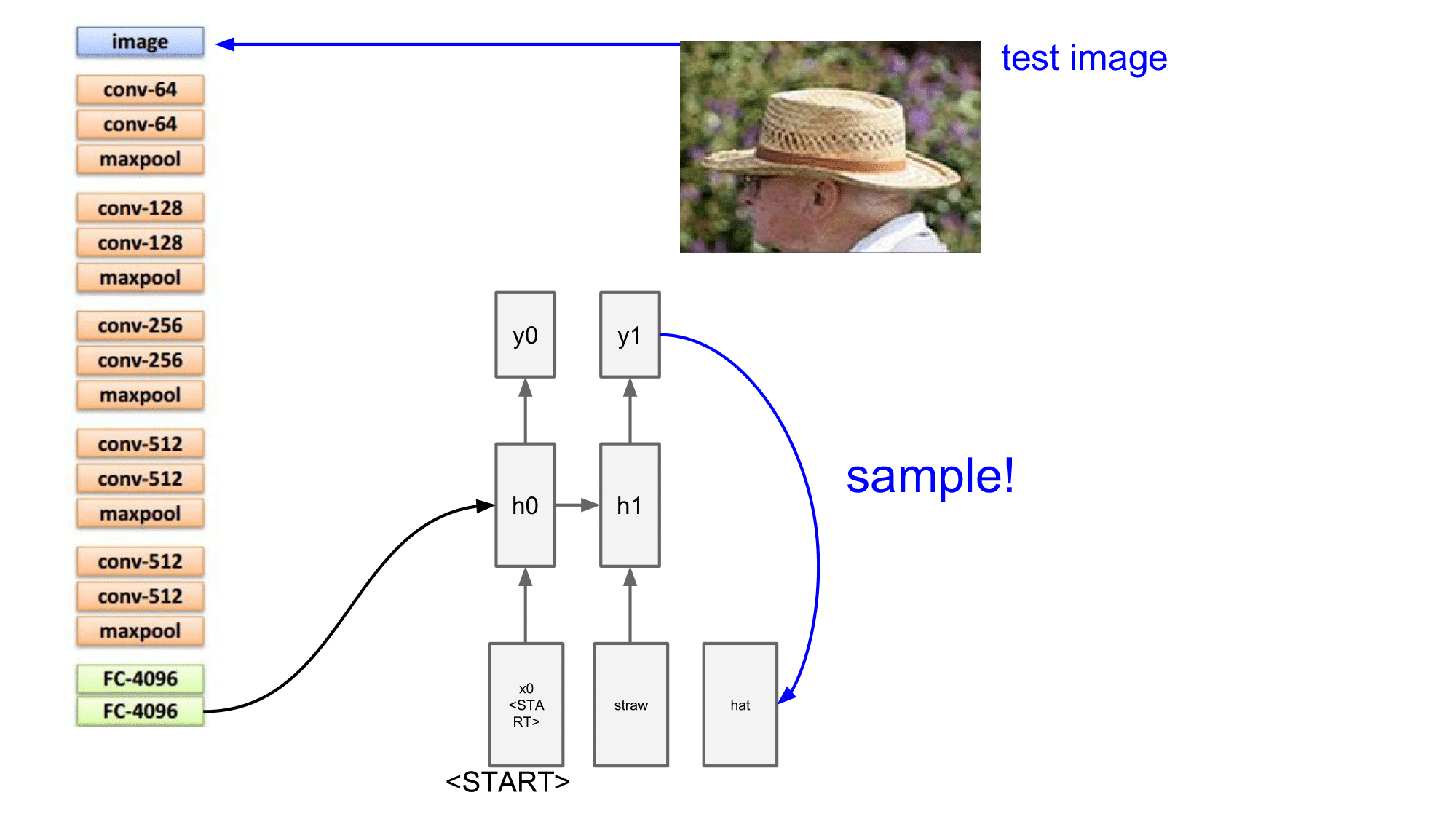
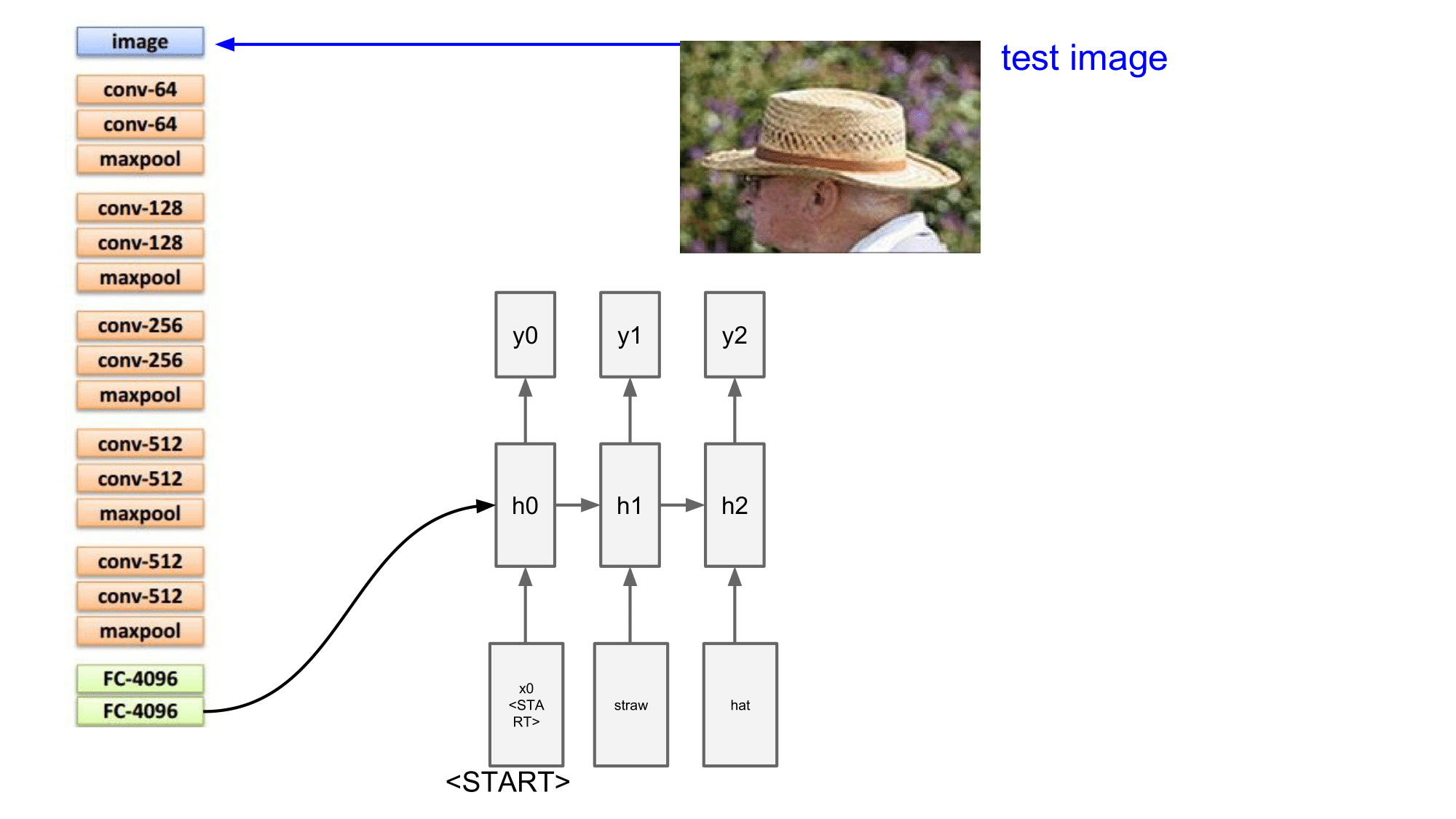
계속해서 이러한 과정을 반복하게 됩니다.
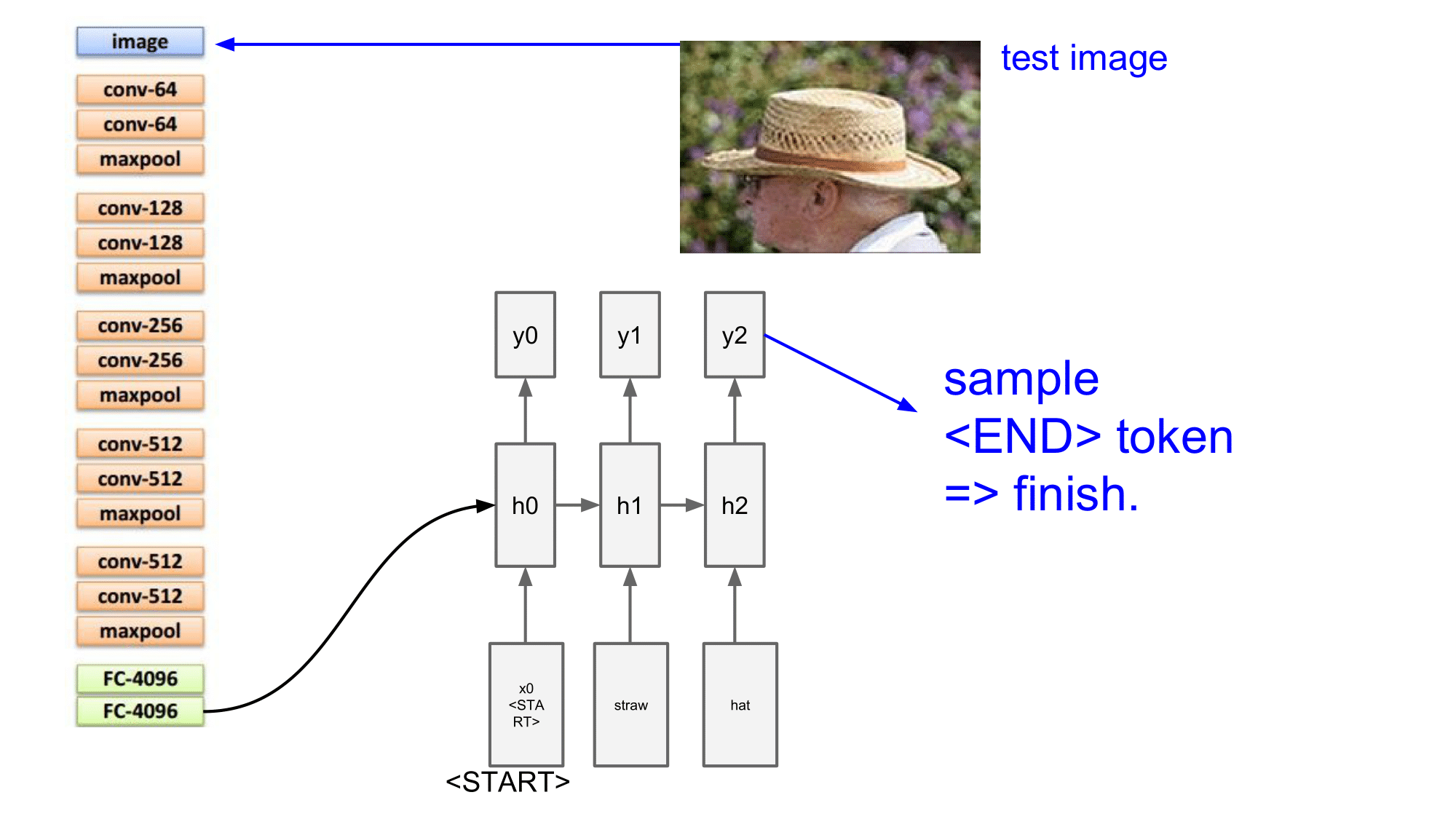
최종적으로 <END> 토큰이 오게 되면 마침표의 역할을 하게 됩니다.
그렇게 해서 최종 결과는 straw hat . 이 되겠습니다.
그리고 마지막에 <END> 토큰이 들어가기 때문에 dimension 관점에서 보게 되면 input 쪽의 dimension + 1 을 한 것이 y 쪽의 dimension 이 되겠습니다.
여기서 한 가지 짚고 넘어가야 할 점은, CNN 과 RNN 이 따로 동작하는 것이 아니라 마치 하나의 단일 모델인 것처럼 동작하여 backpropagation 이 한꺼번에 진행된다는 것입니다.
지금부터는 Image Captioning 을 실험할 수 있는 dataset 들에 대해서 알아보겠습니다.

Image Captioning 에 사용되는 대표적인 dataset 은 Microsoft 의 COCO 입니다. 다음과 같이 이미지들 넣으면 해당 이미지에 대한 Caption 을 생성하게 되는 것을 볼 수 있습니다.

몇 가지 이미지와 잘 안 맞는 caption 도 있긴 하지만 그래도 잘 맞추는 것을 확인할 수 있습니다.
이렇게 RNN 이 좋은 성과를 보이고 있습니다. 여기서 RNN 의 다음은 무엇이냐고 하게 되면 많은 사람들이 attention 이라고 한다고 합니다. attention 은 Lecture 13 에서 segmentation 과 함께 상세히 알아보겠지만, 지금 간단하게 개념만 알아보겠습니다.
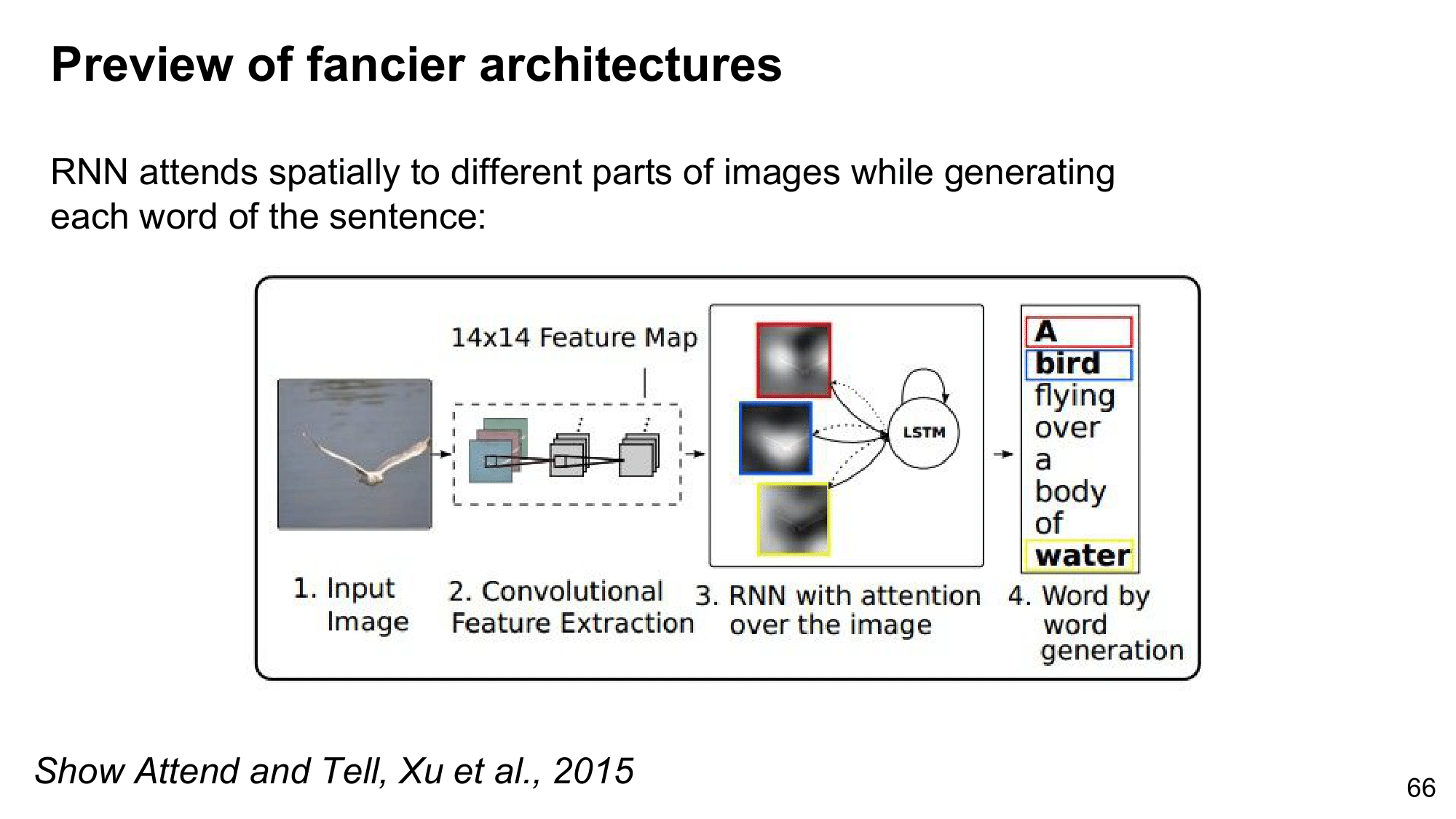
지금 RNN 은 이미지를 전체적으로 한 번만 보고 끝내는 반면에, attention 은 이미지 특정 부분을 보고 그 부분에 적합한 부분을 추출하고, 또 다른 부분을 보고 또 다른 단어를 추출하는 식으로 진행할 수 있습니다. 예시를 보게 되면, 위의 빨간 박스 부분을 보고 A 라는 단어를, 파란색 박스 부분의 흰색 새 부분을 보고 bird를, 노란색 박스의 물 부분을 보고 water를 추출해 내는 것을 볼 수 있습니다.
이처럼 이미지를 한 번에 보는 것이 아니라, 부분 부분을 보면서 문장들을 추출해내는 방식이 되겠습니다. 위의 예시처럼 단순하게 단어를 생성해내는 것이 아니라 다음에 어디를 봐야 하는지도 알려준다고 하여 주목받는 모델로 Show Attend and Tell 이라는 논문에서 발표된 내용입니다.
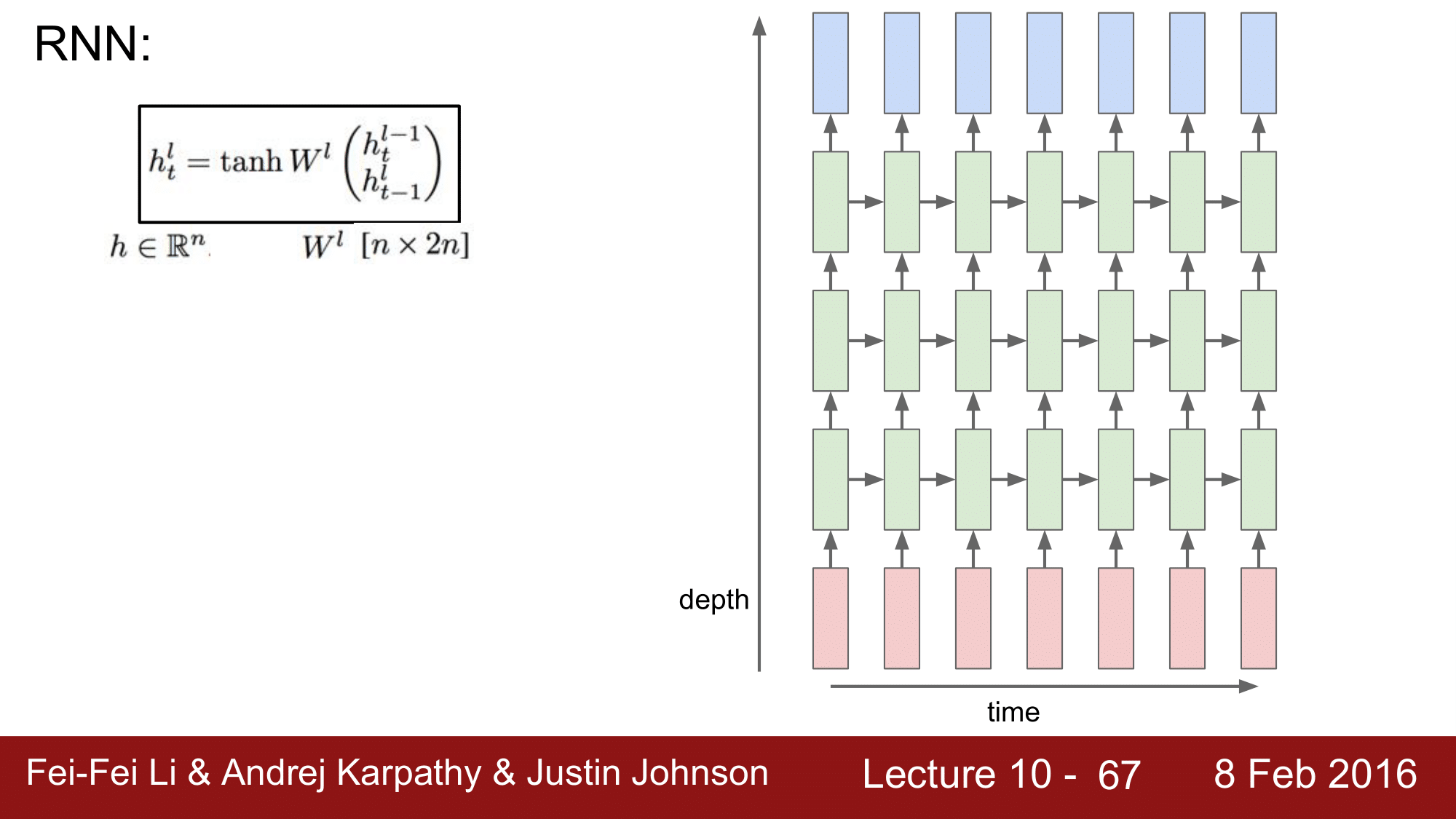
RNN 을 응용한 사례들은 여러 가지가 있습니다.
위의 예시는 원래 하나의 hidden layer 를 가졌던 것을 3개로 stacking 한 것입니다. 위처럼 되면 세로로 봤을 때 Wxh, Whh, Whh, Why 가 되는데 가로로는 같지만 세로로는 각각 다른 것이 되겠습니다.
RNN 은 여러 가지 문제가 있기 때문에 현업에서는 사용되기가 힘듭니다. 그 문제에 대해서는 뒤에서 다로 보도록 하겠습니다.
RNN이 현업에서 사용되기 힘들기 때문에, 대체로 많이 사용되는 것이 LSTM 이라는 것을 사용합니다.
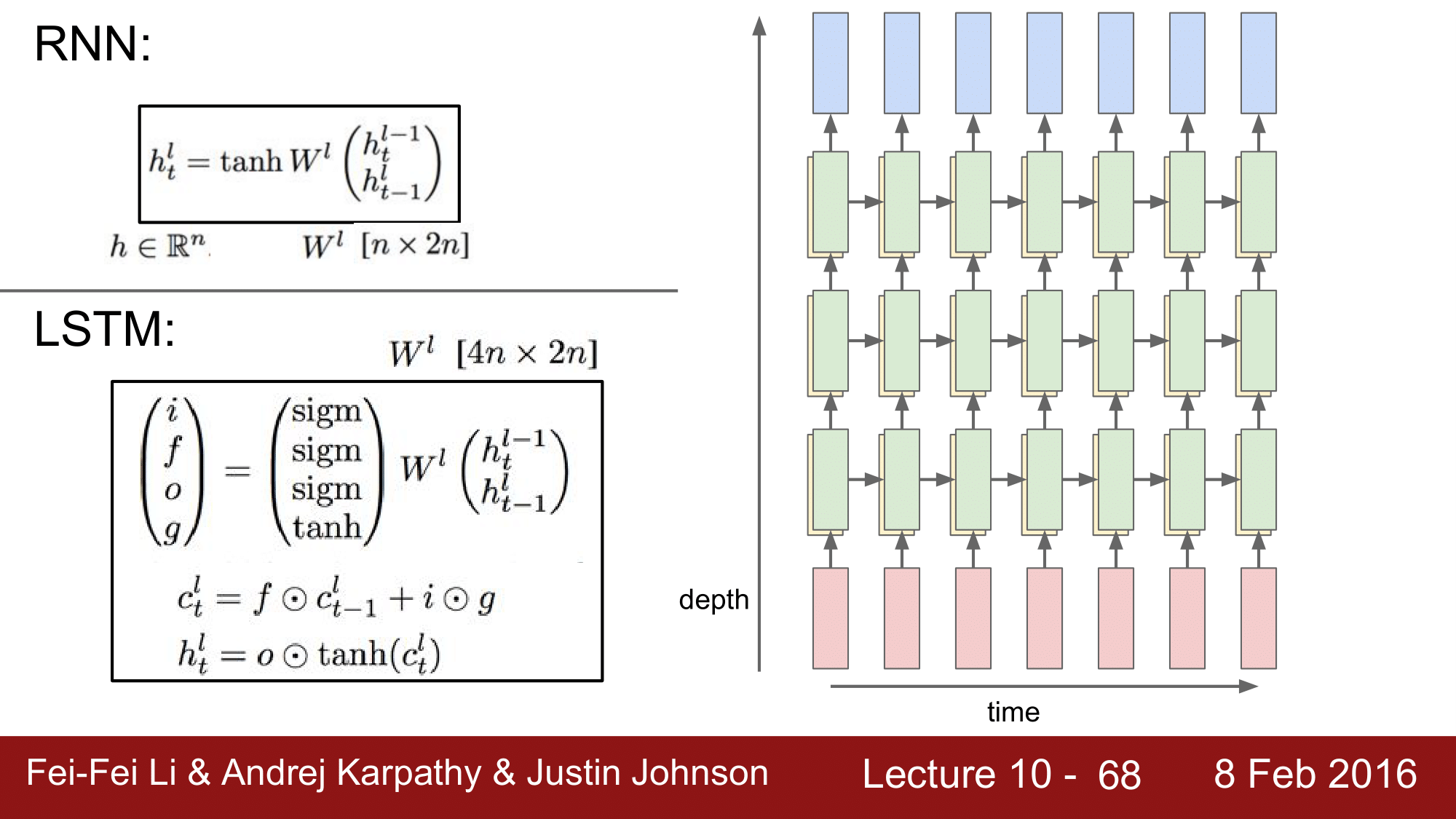
LSTM 의 기본적인 원리는 RNN 과 동일합니다만 차이가 있습니다.
RNN 에서는 hidden state 이 존재했었는데, LSTM 의 경우 오른쪽 그림에서 노란색 부분(cell state)이 함께 존재한다는 것이 근본적인 차이가 되겠습니다. 매 single point 에 hidden state vector 와 cell state vector 두 개가 존재한다는 것으로, cell state vector 는 왼쪽의 식과 같이 표현됩니다.
각각의 cell 에는 input, forget, output, g 라는 게이트가 있습니다. g 를 제외한 게이트들은 sigmoid 로 g는 tanh 로 구성됩니다.
$c_t^l = f \odot c_{t-1}^l + i \odot g$ 에서 $f$ 는 forget 게이트로 현재의 상태(cell state; $c_t^l$)가 바로 직전의 상태($c_{t-1}^l$)을 얼마나 잊을 것이냐를 정해주는 것입니다. 만약 forget 게이트가 1이라면 이전의 상태 전체를 전달해 줄 것이고, 만약 forget 이 0이라면 이전의 상태를 전혀 고려하지 않겠다는 의미가 됩니다. 그리고 $i$ 는 input 값은 sigmoid 이기 때문에 $0 \le i \le 1$, $g$ 는 tanh 이기 때문에 $-1 \le g \le 1$ 가 됩니다. 그래서 input 값을 cell state 에 포함시켜 줄 것인지를 결정하는 것이 $i$ 가 되고 $g$ 는 결국 cell state 에 얼마나 더 더해주겠는가를 결정합니다.
이렇게 해서 현재의 cell state 를 구하게 되면, cell state 를 tanh 의 인자로 넣어주게 됩니다. 이렇게 squash 한 다음에 이를 output 게이트에 곱해줍니다.
결국은 현재의 cell state 를 output 에 반영함으로써 hidden state vector 를 구하게 되는 것입니다.
정리하자면, 노란색의 cell state vector 를 구하고, 이를 초록색 부분으로 전달하여 hidden state vector 를 구하게 됩니다.
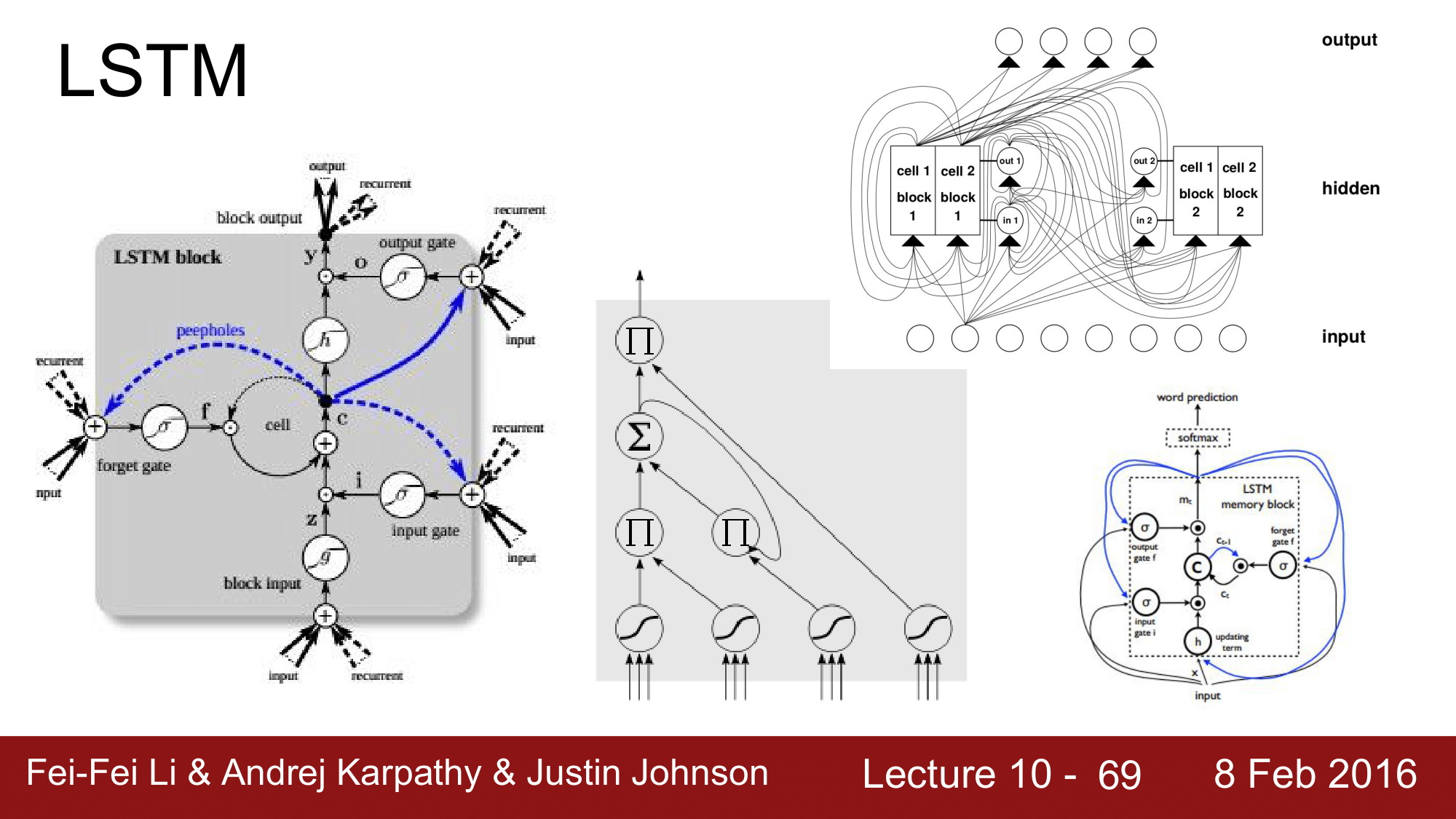
복잡하게 설명드리긴 했지만, 위키피디아를 찾아보게 되면 위와 같이 더 복잡해 보이는 도형들을 만나볼 수 있습니다.
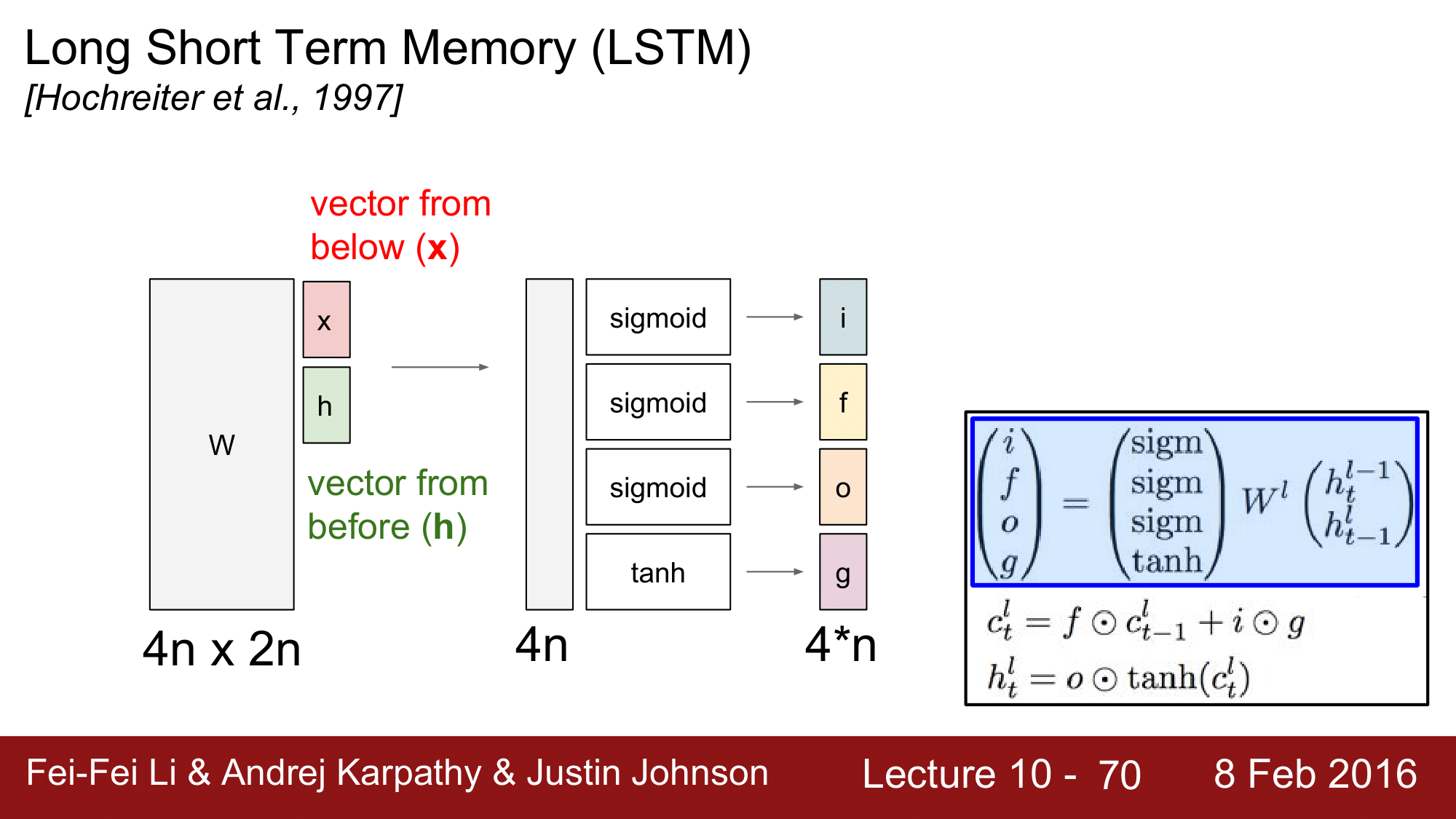
앞에 설명했던 내용을 다시 한번 정리하겠습니다.
input 에서의 vector(x), 전 단계의 hidden vector(h), 두 개를 결합해서 n + n = 2n 이 되고, $(4n, 2n) \times (2n, 1)$ 로 $4n$ 이 되고, 각각이 $(i, f, o, g)$로 할당됩니다. 이후에 f 와 기존의 cell state, i, g 가 영향을 미쳐서 현재의 cell state 를 구하고, 현재의 cell state 를 squash 한 다음 o 와 연산하여 hidden state 를 구하는 것이 요점이 되겠습니다.

LSTM 에서 핵심은 cell state 입니다. cell state 가 화살표방향으로 쭉 흘러가는 모양새를 가지고 있습니다.
그렇게 해서 f 와 이전의 cell state를 연산해 줍니다. 이때 f 가 0이라면 전 state 를 반영하지 않게 됩니다. 즉, cell 자체를 reset 하게 됩니다.
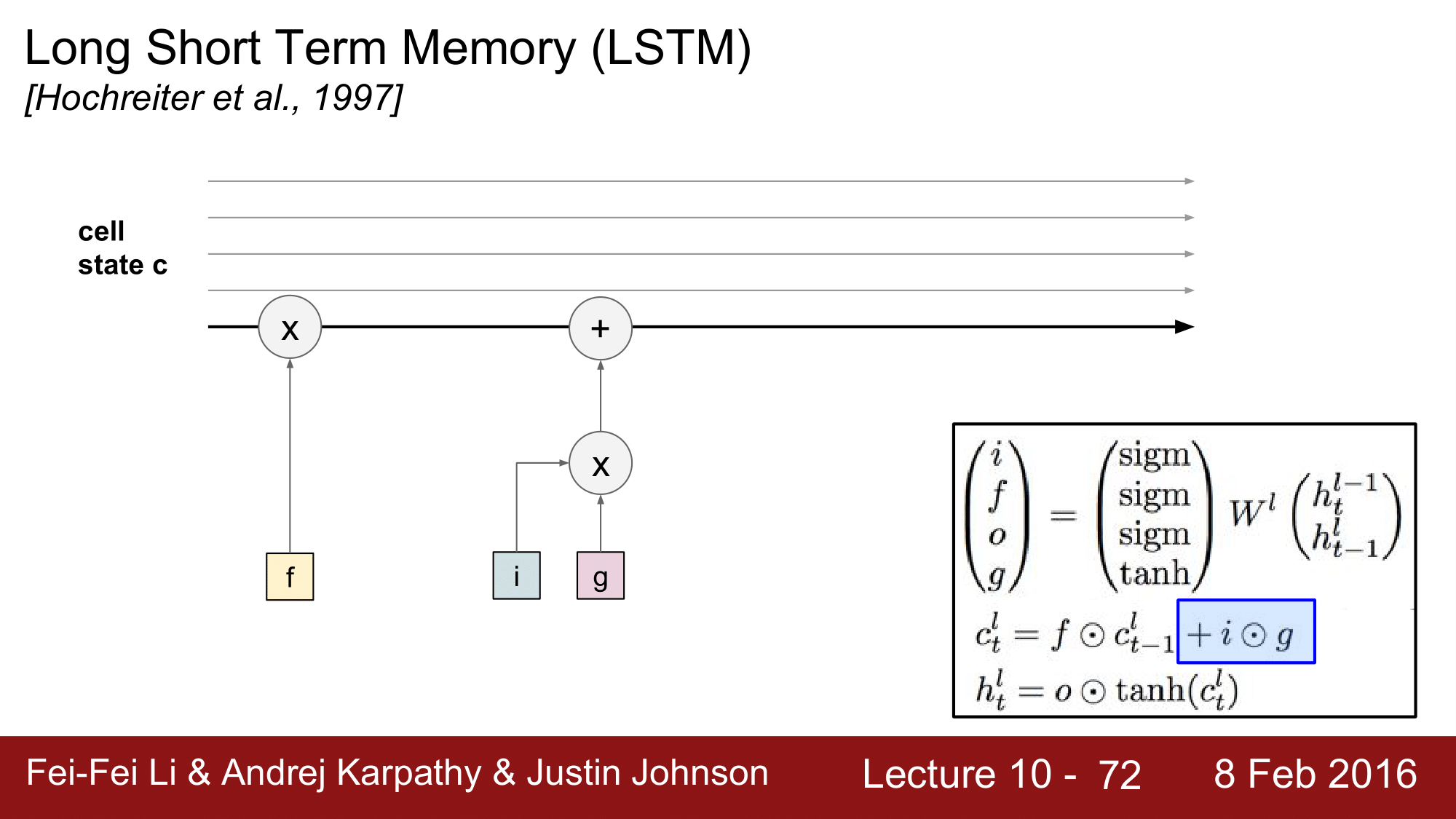
그다음 i 와 g 의 연산 단계에서는 input 값을 현재 cell state 에 어느 정도만큼 더해줄 것인지를 결정하게 됩니다. 여기까지 오게 되면, 현재의 cell state 를 구한 것이 되겠습니다.
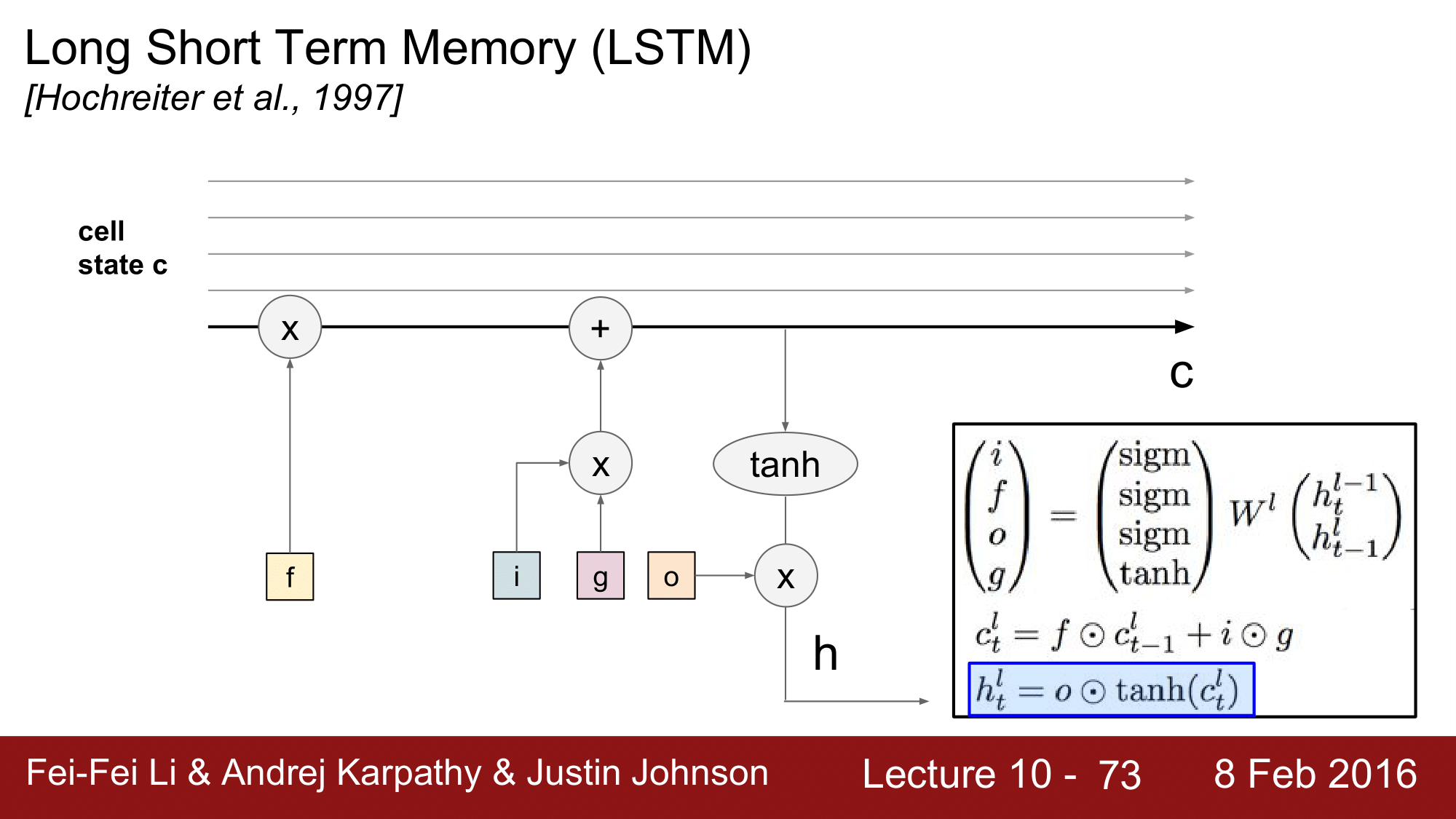
이후 hidden state 를 구하기 위해 tanh 로 현재의 cell state 를 squash 해주고, o를 곱해줍니다.
이렇게 함으로써 hidden state 를 구하게 되는 것인데, 여기서 o 는 다르게 생각하면 현재의 cell state 중에 어느 부분을 다음의 hidden cell 로 전달할지 결정하는 것이 o 라고 할 수 있습니다.
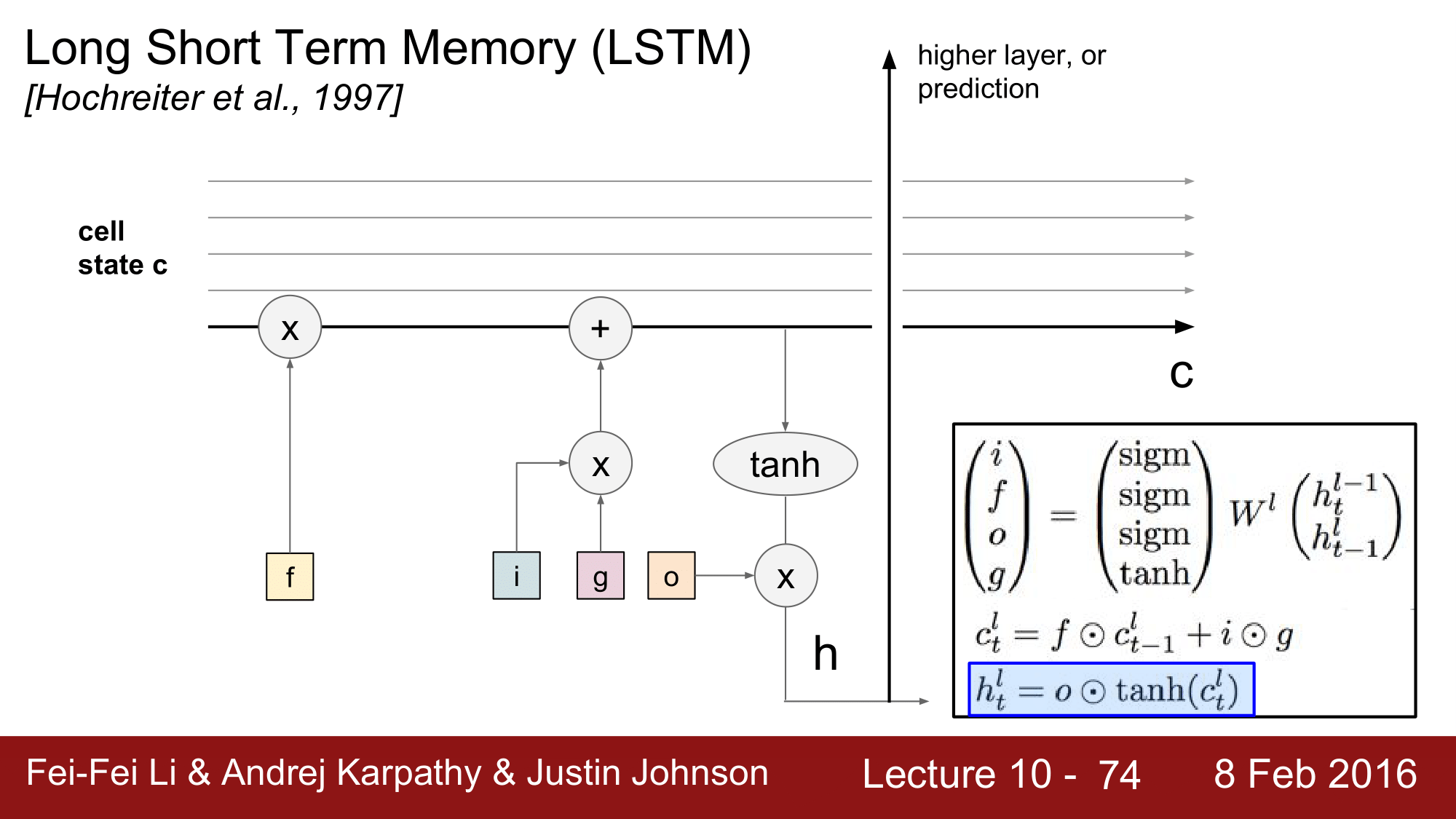
이후 hidden state 는 양갈래길을 가게 됩니다. LSTM 의 다음 iteration 인 오른쪽 방향과, 위의 단계의 레이어로 향합니다. 물론 위 단계의 레이어로 갈 때, 끝으로 가게 되면 prediction 을 하게 됩니다.
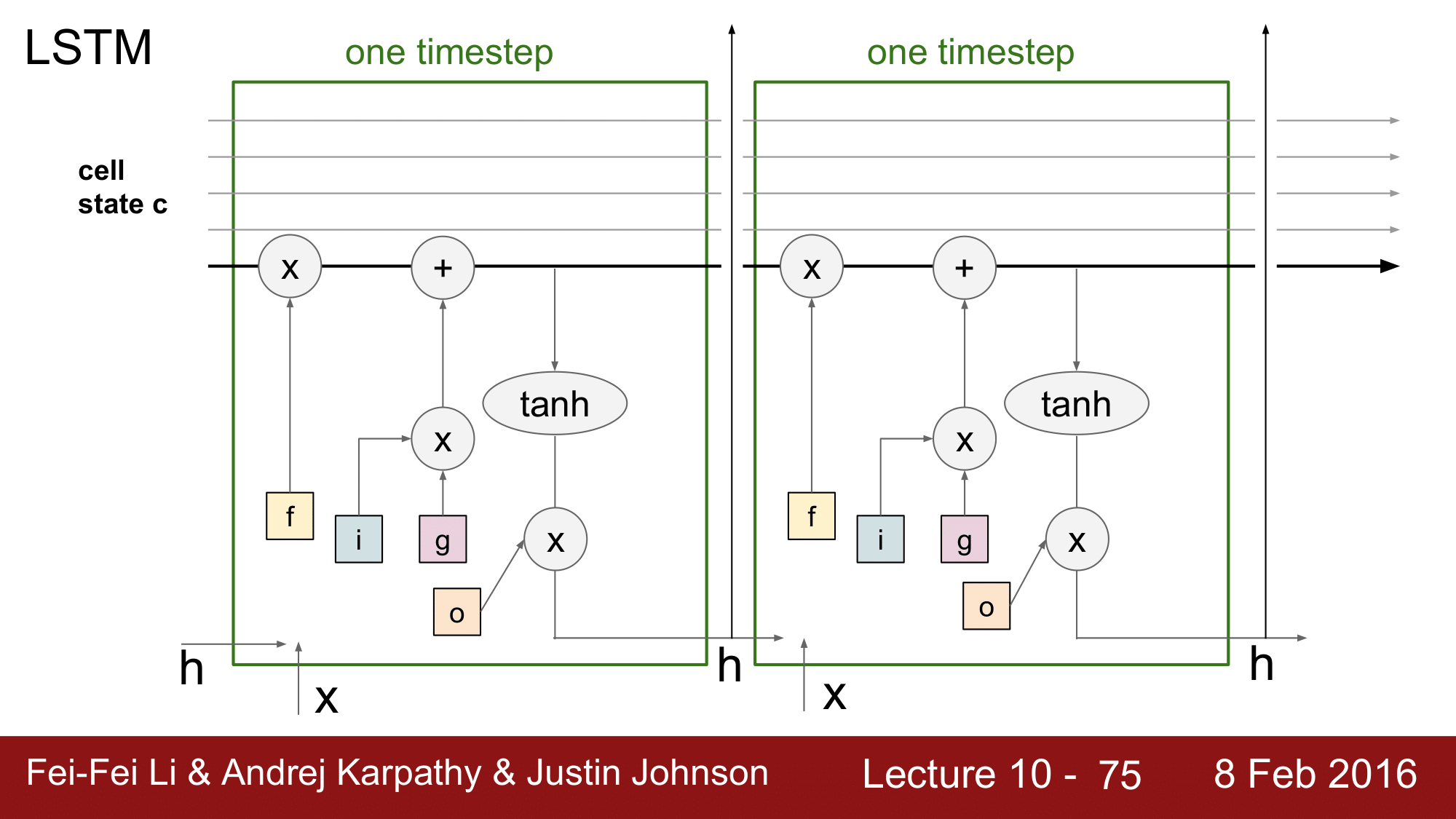
그림으로 다시 풀어서 보게 되면 위와 같이 됩니다.
h 는 위쪽(상위 Layer 또는 prediction)과 오른쪽(LSTM의 다음 iteration)으로 이동하게 됩니다.
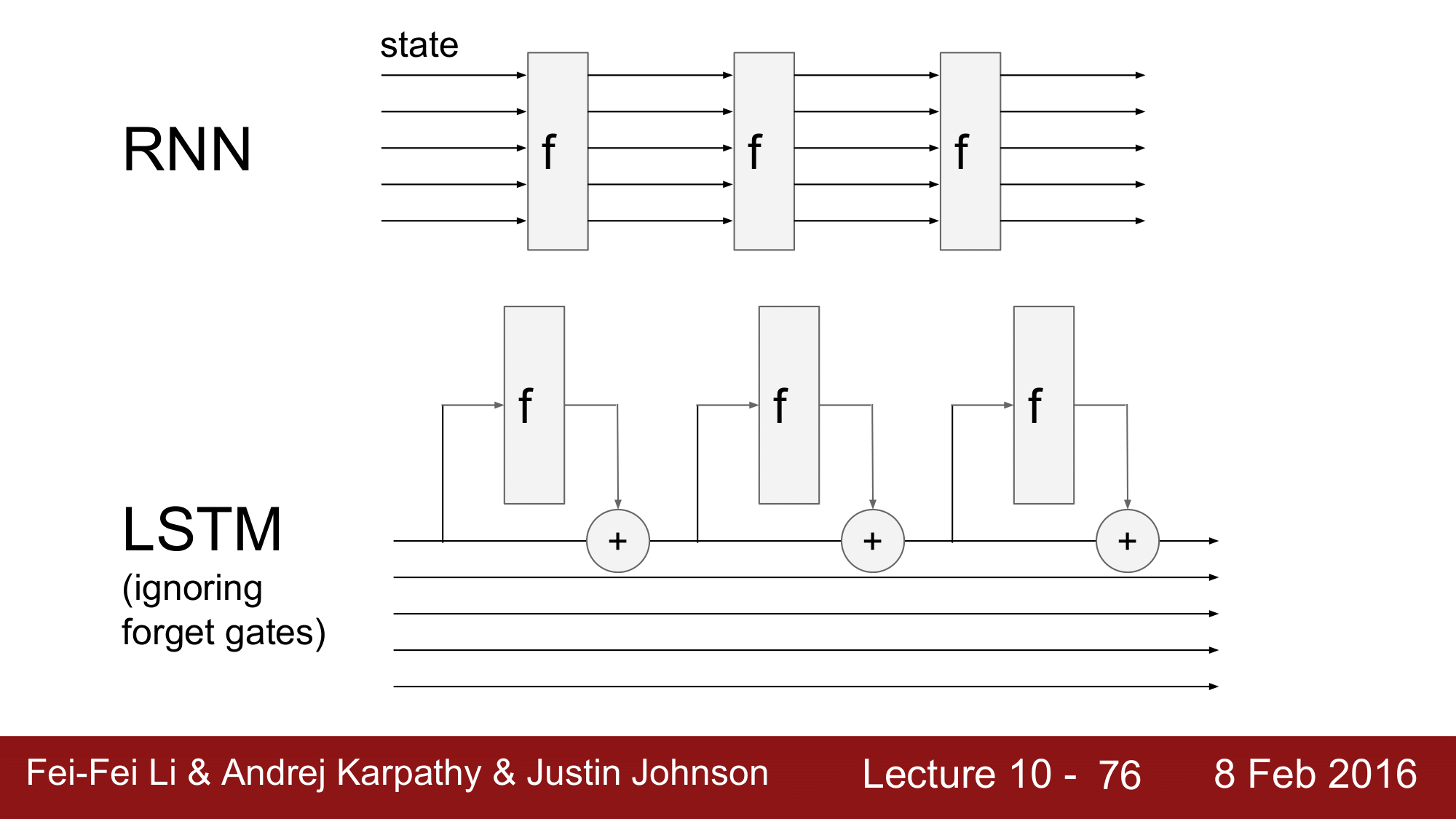
RNN 은 현업에서 사용하지 않는다고 앞서 말했는데, 왜 LSTM 이 RNN 보다 더 좋은 모습을 보이는 지에 대해서 알아보겠습니다.
RNN 에서의 Recurrence formula 를 다시 생각해보면, input x 와 W 를 곱해주고 그 단계의 hidden 과 W 를 곱해준 값을 더해 tanh 를 해준 것이 hidden state 가 됐습니다. 그리고 이 hidden state 에 W 를 곱한 것이 y가 됐습니다.
$h_t = \text{tanh}(W_{hh}h_{t-1} + W_{xh}x_t)$ $y_t = W_{hy}h_t$
이 때, RNN 의 경우 y 가 transformative 하게 급격하게 변화하는 반면, LSTM 에서는 cell state 가 flow 할 때, 세 개의 게이트 forget, input, output 들이 additive 하게 영향을 주어 점진적으로 변화하게 됩니다.
특히 LSTM 에서는 $c_t^l = f \odot c_{t-1}^l + i \odot g$ 에서 $\odot$연산이 들어감으로 인해 결정적인 역할을 하게 됩니다.
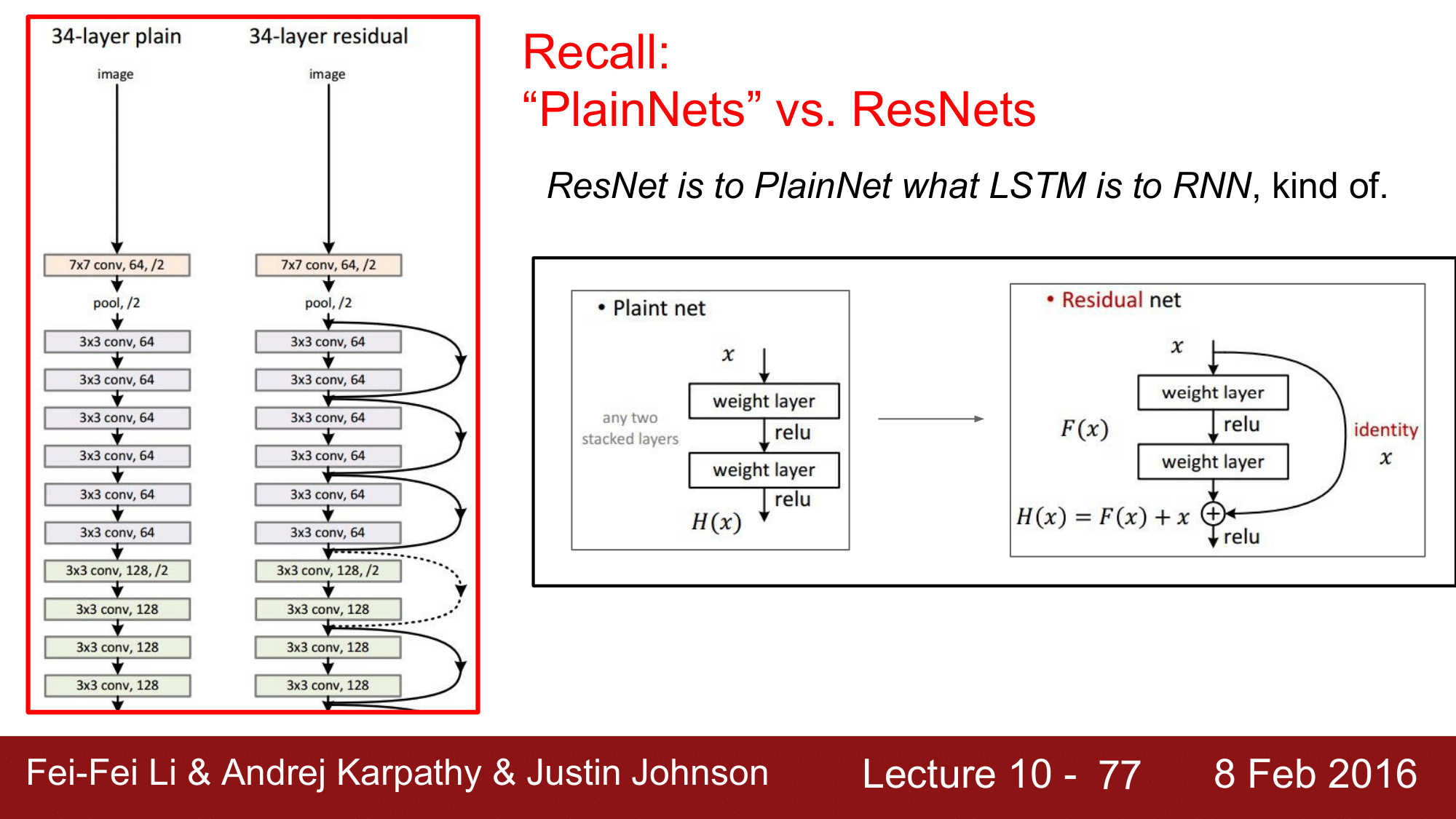
$\odot$연산의 역할을 설명하기 위해, PlainNet 과 ResNet 을 비교해서 보도록 하겠습니다.
ResNet 과 PlainNet 의 관계는 LSTM 과 RNN 의 관계와 같다고 볼 수 있습니다.
ResNet 에는 $\oplus$연산이 들어가고 $H(x) = F(x) + x$ 에서 $+x$ 가 additive 한 interaction 을 수행하는데 이러한 skip connection 들이 LSTM 과 유사한 역할을 하고 있다라고 할 수 있습니다.

RNN 에서는 backward flow 가 굉장히 안 좋습니다. backpropagation 을 수행할 때 vanishing gradient 문제가 발생한다는 것입니다.
위 코드에서 Whh 만 보게 되면, forward pass 를 해주고 backward pass 를 진행하게 되는데, 50 번의 step 을 돌면서 50 번의 dot product 연산을 수행하게 되는데 Whh 에 동일한 수를 계속해서 곱하게 되면, eigenvalue 가 1보다 크면 explode 할 것이고, 1보다 작으면 vanish 하게 될 것입니다.
A * v = lamda * v

그래서 RNN 에서 backpropagation 을 진행하게 되면 언제나 vanish 문제가 발생할 수 있습니다. 이를 방지하기 위해, [-5, 5]의 범위를 넘어가면 gradient clipping 을 해주거나 일반적인 경우 LSTM 을 사용하여 vanish 문제를 해결합니다.
LSTM 에서는 back propagation 을 할 때, $+$ 연산을 해줍니다. $+$ 연산은 backward pass 때 distributor 역할을 해주기 때문에 gradient 를 그대로 앞단으로 전달하여 super highway 와 같은 역할을 해주게 됩니다. 그래서 LSTM 의 경우 $+$ 연산에 의해 gradient 를 앞 단으로 그대로 전달해 주기 때문에 vanishing gradient 같은 문제가 발생하지 않게 됩니다.
물론, 이때 forget 게이트를 생각하게 된다면 달라질 수 있습니다. forget 게이트로 cell state 를 잊겠다고 해서 0을 주게 된다면, 그 지점에서 gradient 의 진행이 멈춰버리기 때문에 멈추지 않도록 하기 위해서 forget 게이트에 bias 를 도입하여 완전히 0이 될 수 없도록 합니다. 이렇게 gradient 가 완전히 진행을 멈추는 경우는 없도록 하는 방법도 있습니다.
LSTM 의 변형

LSTM 은 다양한 변형된 모델도 가지고 있습니다.
2015 년의 LSTM: A Search Space Odyssey 에서는 굉장히 다양한 실험을 하였는데, 결과적으로는 이 논문에서의 실험이 주목할만큼의 성능 차이를 보이지 않았다는 내용입니다.
그리고 NYU 의 조경현 교수님이 2014년에 발표하신 Learning phrase representations using rnn encoder-decoder for statistical machine traslation 에서는 GRU 에 대해서 소개합니다.
GRU 는 LSTM 과같이 많이 사용되는 것으로 LSTM 보다 식이 조금 더 간단하면서도 좋은 성능을 내는 모델이라고 할 수 있습니다. 일단 GRU 는 cell state 없이 hidden state 만 있는 모습으로 구현한다 정도만 알고 넘어가면 될 것 같습니다.
정리

